Билинейные и квадратичные формы. Приведение квадратичной формы к каноническому виду. Метод Лагранжа, страница 3

где g( y₂,…, y_n) - квадратичная форма  от не более чем n -1 неизвестной. Преобразование (3) невырожденное, так как матрица этого преобразования равна

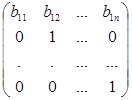, и определитель равен b₁₁ ¹ 0. Обратное ему преобразование тоже невырожденное и приводит форму f в форму (4). По индуктивному предположению квадратичную форму g( y₂,…, y_n) невырожденным преобразованием переменных   y₂,…, y_n можно привести к квадратичной форме канонического вида. Это преобразование можно рассматривать как невырожденное, при котором неизвестная y₁ остается без изменения. Оно приводит квадратичную форму (4) к каноническому виду. Таким образом, невырожденным преобразованием переменных форма  f  приводится к каноническому виду.

2. Все диагональные коэффициенты b₁₁, b₂₂, …, b_nn равны нулю. Тогда среди коэффициентов формы должен быть отличный от нуля. Так как в противном случае форма тождественно равна нулю и являлась бы канонической. Пусть, например, b₁₂  ¹ 0.  Сделаем вспомогательное преобразование переменных так, чтобы в квадратичной форме появился квадрат. Сделаем преобразование переменных:

x₁ = z₁ + z₂, x₁ = z₁ -  z₂,  x₃ = z₃,…, x_n = z_n.

Оно невырожденное, так как матрица этого преобразования равна

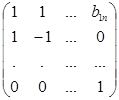, и определитель ее равен 2 и не равен нулю. В результате этого преобразования член нашей формы примет вид

2 a₁₂x₁x₂ = 2 a₁₂( z₁ + z₂)(z₁ -  z₂) = 2 a₁₂z₁² - 2 a₁₂ z₂², и форме появляется ненулевой коэффициенты у квадратов двух переменных. Эти члены не могут сократиться с остальными членами, так как во все остальные члены войдет хотя бы одна из переменных z₃,…, z_n. Полученную квадратичную форму по первой части доказательства можно привести к квадратичной форме канонического вида невырожденным преобразованием переменных. 

Пример. Методом Лагранжа привести квадратичную форму к каноническому виду

, и найти преобразование переменных, приводящую эту форму к каноническому виду.

Решение. Так как в форме нет квадратов переменных, то сделаем преобразование переменных

x₁ = z₁ + z₂, x₁ = z₁ -  z₂,  x₃ = z₃

Матрица этого преобразования равно

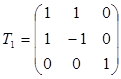
и квадратичная форма преобразуется к виду

.

Выделим полный квадрат из членов, содержащих x₁

.

Полагаем y₁ =z₁ +(5/2)z₃, y₂ = z₂+(1/2) z₃,  y₃ = z₃ приведем квадратичную форму к каноническому виду

.

Выразим неизвестные z₁ =y₁ - (5/2)y₃,  z₂ = y₂-(1/2) y₃,  z₃ = y₃. Последнее преобразование имеет матрицу

.

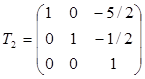Тогда преобразование, переводящее данную квадратичную форму к форме канонического вида имеет матрицу, равную произведению матриц .

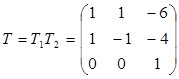, преобразование переменных имеет вид:

x₁ =y₁ + y₂  - 6y₃, x₂ =y₁ - y₂  - 4y₃,   x₃ = y₃.

4.  Закон инерции квадратичных форм.Квадратичную форму можно привести к каноническому виду различными способами.

Определение 1. Канонический вид квадратичной формы называется нормальным видом квадратичной формы, если все ее неравные нулю коэффициенты равны +1 или -1.

Теорема 1. Любую квадратичную форму с действительными переменными  невырожденным линейным преобразованием переменных можно привести к нормальному виду.

Доказательство. Приведем сначала квадратичную форму к каноническому виду (2) §3. Можно предположить что в полученной квадратичной форме канонического вида имеется r коэффициентов неравных нулю, среди которых имеется s положительных коэффициентов и t отрицательных коэффициентов. При этом можно неизвестные перенумеровать и форму канонического вида представить в виде:

, где 0 £ s £ r £ n и все коэффициенты с₁, с₂,…, с_r положительны. Тогда невырожденное преобразование переменных

приводит форму f  к нормальному виду,

.

Определение 2. Рангом квадратичной формы называется ранг матрицы квадратичной формы.

Определение 3. Число s положительных коэффициентов в каноническом виде квадратичной формы называется положительным индексом инерции формы, число t отрицательных коэффициентов - отрицательным индексом инерции формы. Упорядоченная пара (s, t) называется сигнатурой квадратичной формы.

Теорема 2. При невырожденных линейных преобразованиях переменных ранг квадратичной формы не меняется. Ранг квадратичной формы равен числу ненулевых коэффициентов в форме канонического вида, т.е. rang  f = s+ t .

Лемма 1. Ранг произведения AB матриц не превосходит ранга каждого из его сомножителей.