










Мы начинаем изучать математический анализ функций нескольких действительных переменных. Переход от случая одной переменной к случаю двух и большего числа переменных не совершается автоматически. Основные понятия – предел, производная, интеграл – приобретают здесь новые свойства и качества. Тем не менее, аналогия с более простым (и уже изученным) случаем нам очень поможет. Важно и то, что многие понятия и факты, рассматриваемые здесь для функций n переменных, при n = 1 нам известны.
Функцией n переменных называется отображение
f : D ® R , где R – поле действительных чисел, D – подмножество в Rn = { (x1,..., xn ) | xiÎR }. Таким образом, функция f = f(x1,...,xn) считается заданной, если задан закон, позволяющий для каждого упорядоченного набора чисел (x1,...,xn)ÎD находить единственное значение f(x1,...,xn)ÎR.
9.1 Множества в n–мерном евклидовом пространстве
9.1.1 Пространство Rn. Областью определения всякой функции n переменных является некоторое множество упорядоченных наборов чисел, т. е. подмножество в Rn.Поэтому начинать изучение таких функций нужно со знакомства с некоторыми видами подмножеств в Rn,с изучения их свойств.
Напомним, прежде всего, известные читателю сведения о самом пространстве Rn. Множество Rn состоит из всех упорядоченных наборов действительных чисел:
Rn = R´R´...´R = { (x1, x2,..., xn) | xiÎR }, т. е. является декартовым произведением n экземпляров множества R (см. АГ, раздел 1.1).
После введения операций сложения и умножения на число:
(x1, x2,..., xn) + (y1, y2,..., yn) = (x1+y1, x2+y2,..., xn+yn),
l(x1, x2,..., xn) = (lx1,lx2,...,lxn)
множество Rn становится линейным пространством (АГ, 3.1, 3.3).
Далее, в пространстве Rn вводится скалярное произведение. Если x = (x1,..., xn), y = (y1, y2,..., yn) –элементы Rn,то их скалярным произведением называется число
(x, y) = x1y1+x2y2+...+xnyn.
Конечномерное линейное пространство со скалярным произведением называется евклидовым пространством (АГ, 4.5, 7.5.1). Скалярное произведение позволяет ввести понятие модуля элемента Rn :
![]() , а также понятие расстояния
между элементами Rn :
, а также понятие расстояния
между элементами Rn :
![]() .
.
В разделе АГ, 4.5 было доказано неравенство Коши–Буняковского:
![]() , справедливое для любых x, y Î Rn . Это неравенство позволяет
определить угол между элементами x, y :
, справедливое для любых x, y Î Rn . Это неравенство позволяет
определить угол между элементами x, y :
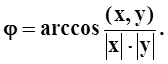
Установим справедливость ещё одного важного неравенства – «неравенства треугольника»:
![]()
Для доказательства проведём равносильные преобразования, используя определение модуля и свойства скалярного произведения:
![]()
![]()
![]()
Справедливость последнего соотношения следует из неравенства Коши – Буняковского.
Замечание. При n = 2, n = 3 имеются хорошие геометрические интерпретации: элементы пространства R2 удобно изображать точками плоскости, а элементы R3 – точками трёхмерного пространства (после введения на плоскости и в пространстве прямоугольных декартовых систем координат). Изучая подмножества в Rn , мы всегда будем обращаться к этим наглядным случаям. Очень часто можно разобраться в ситуации при n = 2, рассматривая множества на плоскости и определённые на них функции двух переменных, а затем перейти к общему случаю с помощью аналогии.
9.1.2 Открытые и замкнутые множества. Пусть aÎRn. Окрестностью (или e–окрестностью) точки a называется множество
Ue(a) = { xÎRn | | x–a | < e }.
Ясно, что при n = 1 это известная нам окрестность точки на числовой прямой – интервал (a–e, a+e). При n = 2 это круг с центром a и радиусом e, не включающий границу, при n = 3 – шар с центром a радиусом e, не включающий ограничивающую его сферу.
 Пусть MÍRn.
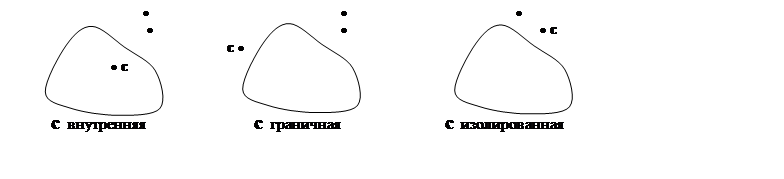
Точка с называется внутренней
точкой множества M, если
существует окрестность Ue(с), целиком лежащая в M. Если любая Ue(с) содержит и точки множества M, и точки, не лежащие в M, то с называется
граничной точкой M.
Множество всех граничных точек называется границей множества M. Если существует Ue(с),
которая содержит только одну точку M
– саму точку c, то такая точка
называется изолированной.
Пусть MÍRn.
Точка с называется внутренней
точкой множества M, если
существует окрестность Ue(с), целиком лежащая в M. Если любая Ue(с) содержит и точки множества M, и точки, не лежащие в M, то с называется
граничной точкой M.
Множество всех граничных точек называется границей множества M. Если существует Ue(с),
которая содержит только одну точку M
– саму точку c, то такая точка
называется изолированной.
Множество, все точки которого являются внутренними, называется открытым. Множество, дополнение к которому (т. е. Rn \ M) открыто, называется замкнутым. Замкнутые множества можно определять также с помощью понятия граничной точки.
Лемма 1.Множество M замкнуто Û M содержит все свои граничные точки.
Доказательство.
«Þ». Пусть M замкнуто, с – граничная точка M. Если cÏM, то c лежит в дополнении к M. Но дополнение открыто, поэтому существует Ue(с),целиком лежащая в дополнении. Это противоречит определению граничной точке. Значит, сÎM.
 «Ü». Пусть M содержит
все свои граничные точки. Возьмём cÏM. Тогда с
не является граничной, т. е. существует Ue(с), не пересекающаяся с M. Значит, любая точка дополнения является
в нем внутренней, т. е. дополнение открыто. Следовательно M замкнуто.
«Ü». Пусть M содержит
все свои граничные точки. Возьмём cÏM. Тогда с
не является граничной, т. е. существует Ue(с), не пересекающаяся с M. Значит, любая точка дополнения является
в нем внутренней, т. е. дополнение открыто. Следовательно M замкнуто.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.