Функции нескольких переменных. Множества в n-мерном евклидовом пространстве, страница 3

Пусть  MÍRⁿ. Точка  c называется предельной  точкой множества М, если в любой её окрестности есть точки M , отличные от c. Сравнивая это определение с определениями внутренней и граничной точек, видим, что предельными являются все внутренние и все граничные точки множества, кроме изолированных. Название «предельная»  оправдано следующим свойством.

Теорема 4.

c–предельная точка множества  M     Û    c = lim x_k,  где  x_kÎM,   x_k ¹ c    ("k).

Доказательство.

« Þ ».Возьмём окрестности точки  с,  радиусы которых стремятся к нулю. В каждой из них есть точки множества М, не совпадающие с  с.  Выберем последовательность таких точек  {x_k}  так:

Тогда  lim x_n = c,  так как ,  а значит  "k³k₀   x_kÎU_e(c).

« Ü ».Пусть  lim x_k = c,  т.е.  Это значит, что любая  e–окрестность точки  с  содержит все  x_k,  начиная с некоторого – в частности, имеет непустое пересечение с  М.

Замечание. Каждая точка cÎM является или предельной точкой М, или изолированной. С другой стороны, предельная точка может и не принадлежать самому множеству. Из леммы 1 следует:

 М   содержит все свои предельные точки     Û      М   замкнуто .

9.1.4. Компактные и связные множества.Множество MÍRⁿ называется компактным, если оно ограничено и замкнуто.

Теорема 5 (критерий компактности). М компактно Û любая последовательность точек  М  содержит сходящуюся подпоследовательность, предел которой принадлежит также  М.

Доказательство.

« Þ ». Возьмём последовательность  {x_k},  x_kÎM.  Так как  М  ограничено, то и {x_k} –ограничена. Значит, по теореме Больцано–Вейерштрасса, можно найти сходящуюся подпоследовательность .  Пусть  .  По теореме 4,  a – предельная точка М.   Но  М  замкнуто, поэтому   aÎM.

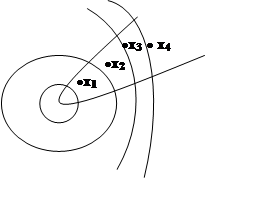
« Ü ». Докажем, что  М ограничено. Допустим, что это не так, т.е.  М  не лежит ни в какой (даже очень большой) окрестности  Возьмём  x₁ÎM,  ; x₂ÎM, ;и так далее: . Способ построения последовательности {x_k} показывает, что любая подпоследовательность в ней не ограничена, а значит расходится.  Это противоречит условию.

Докажем,   что   М   замкнуто.   Пусть   a  – предельная точка  М.   По  теореме  4,   a = limx_k,  где   x_kÎM.    Но тогда любая  подпоследовательность в  {x_k}  тоже стремится к  а.  Используя условие теоремы, получаем, что  аÎМ.  Итак, все предельные точки принадлежат  М,  т.е.  М  замкнуто. Теорема доказана.

Рассмотрим  n  непрерывных функций, определённых на отрезке  [a,b]:

Множество точек

называется  непрерывной  кривой  в   Rⁿ.Точки     a = ( j₁(a),j₂(a),...,j_n(a) ),

b = (j₁(b),j₂(b),...,j_n(b))   называются концами этой кривой. Напомним, кривые в  R³ и в  R²  подробно рассматривались в 7.5.3.

Множество  MÍRⁿ  называется связным  (или линейно связным), если для любых точек  a, bÎM  существует непрерывная кривая с концами  a, b, целиком лежащая в  М.

9.2    Предел функции нескольких переменных

В самом начале этого модуля уже был дан ответ на вопрос, что такое функция нескольких переменных. В основном, мы будем работать с функциями, заданными аналитически (т.е. формулой). Например:

Графический способ задания возможен только для функции 2–х переменных. Графиком функции f(x,y) с областью определения D называется множество точек в пространстве  R³

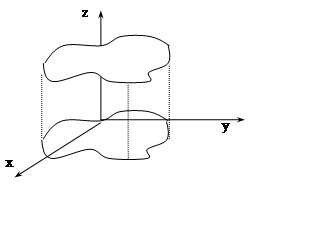
Если область определения D расположить в плоскости XOY, а значения функции откладывать по оси OZ, то график в общем случае представляет собой поверхность.

Пример 1. Рассмотрим функцию . Её область определения:

 – круг радиуса 1 с центром в начале координат. Графиком является верхняя полусфера     x² + y² + z² = 1 ,  z ³ 0 .

Перейдём к определению предела функции. Пусть функция f определена на множестве  DÍRⁿ,  P_o –предельная точка множества  D. Число  b  называется пределом функции  f  в точке  P_o,  если