Функции нескольких переменных. Множества в n-мерном евклидовом пространстве, страница 5

Теорема 7 .  Сумма, разность, произведение, частное непрерывных в данной точке функций  являются снова непрерывными функциями (если только знаменатель не обращается  в  0 ).

Пример 5 .  Исследовать на непрерывность функцию      .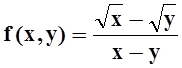

Решение. Функция определена и непрерывна во всех точках 1–й четверти , кроме точек прямой  y = x.  Точки этой прямой (при x ³ 0) являются предельными для области определения  f.  Значит, это точки разрыва.

Заметим, что при  a ¹ 0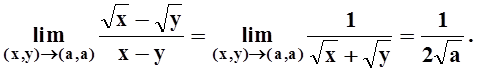    

Доопределяя функцию равенством 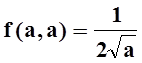  ,  можно сделать её непрерывной в таких точках, разрывы можно назвать устранимыми. Исключение составляет точка (0,0):

.

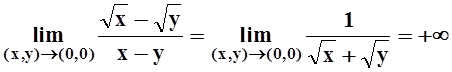В формулировке следующей теоремы содержится новое понятие сложной функции нескольких переменных.

Теорема 8. Пусть функции  g₁, g₂,..., g_k  непрерывны в точке  P_o  пространства  Rⁿ. Пусть в окрестности точки (g₁(P_o), g₂(P_o),..., g_k(P_o)) пространства R^k определена и непрерывна функция  f.  Тогда сложная функция   f(g₁(P), g₂(P),..., g_k(P))   непрерывна в точке  P₀.

Доказательство. Используем определение предела на языке последовательностей. Пусть  B₁, B₂, B₃,...– последовательность точек пространства  Rⁿ,  сходящаяся к  P_o.  Так как функции  g₁, g₂,..., g_k  непрерывны в точке  P_o, то  , i =1,2,...,k. Рассмотрим последовательность точек в пространстве  R^k:

C₁ = ( g₁(B₁),  g₂(B₁),..., g_k(B₁) ),

C₂ = ( g₁(B₂),  g₂(B₂),..., g_k(B₂) ),

C₃ = ( g₁(B₃),  g₂(B₃),..., g_k(B₃) ),

………………………………  .

Их первые координаты, как мы установили, сходятся к числу  g₁(P_o), вторые координаты сходятся к числу  g₂(P_o)  и т.д. Применим теорему о покоординатной сходимости и получим, что

Отсюда и из непрерывности функции   f :  R^k®R   вытекает, что

Итак, доказано, что для любой последовательности   B_j ® P_o

, что и означает непрерывность сложной функции.

В теории непрерывных функций одной переменной  важную роль играли свойства функций, непрерывных на отрезке [a,b]: также функции ограничены, достигают своих точных верхней и нижней граней, принимают все промежуточные значения, равномерно непрерывны (теоремы 3, 5, 6, 12  из 3 модуля). Рассмотрим аналогичные свойства функций нескольких переменных.

Будем говорить, что функция  f  непрерывна на множестве D, если она непрерывна в каждой точке этого множества.

Теорема 9. Если функция f непрерывна на компактном  множестве D, то она ограничена на  D  и достигает своих точных верхней и нижней граней.

Доказательство. Допустим, что f не ограничена. Тогда существует последовательность точек  {P_k},  P_kÎD,  такая, что  . Используем критерий  компактности (теорема 5 из 9.1.4): существует подпоследовательность  По определению непрерывной функции, тогда  – противоречие с тем, что . Следовательно, f ограничена.

Из ограниченности  f  следует, что множество её значений  f(D) = {f(P) | PÎD}  – ограниченное множество чисел. Значит, у него есть точные верхняя и нижняя грани. Рассмотрим подробно  .  По определению, в любой окрестности числа  m есть числа из множества  f(D),  т.е.  m – предельная точка множества  f(D).  Поэтому существует последовательность {f(B_k)}, сходящаяся к m. Рассмотрим {B_k} – последовательность точек D. По критерию компактности, в ней существует подпоследовательность {B_ki}: . Из непрерывности f следует, что .  Но если  ,  то    предел   любой   подпоследовательности  тоже  равен  m.   Поэтому    m= f(B), точная верхняя грань достигается. Аналогично доказывается, что  .

Теорема 10 (о промежуточных значениях). Пусть функция  f непрерывна на связном множестве  EÍRⁿ.  Возьмём любые  A, B ÎE.  Если  f(A) £ k £ f(B),  то существует  CÎE : f(C) = k.  Другими словами, все промежуточные значения достигаются.