









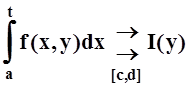 ,
т.е. "e>0 $U(b) (окрестность точки x=b ): "tÎU(b),"yÎ[c,d]
,
т.е. "e>0 $U(b) (окрестность точки x=b ): "tÎU(b),"yÎ[c,d]
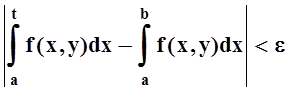 .
.
Пример
9. Рассмотрим интеграл 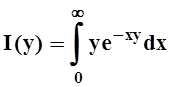 , где yÎ[0,¥). Он сходится в
каждой точке yÎ[0,¥).
Действительно, если y= 0, то и I(y)= 0. Пусть y¹0:
, где yÎ[0,¥). Он сходится в
каждой точке yÎ[0,¥).
Действительно, если y= 0, то и I(y)= 0. Пусть y¹0:
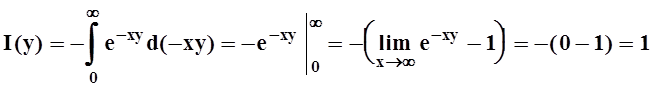 .
.
Возьмём какое–либо число c> 0 и покажем, что на промежутке [c,¥) наш интеграл сходится равномерно. Обозначим:
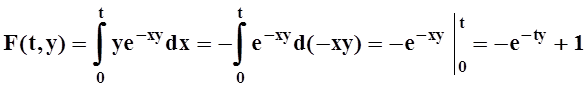 .
.
Требуется доказать, что 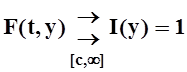 , т.е.
, т.е.
"e>0 $M: "t> M,"yÎ[c,¥)|F (t,y) – I(y) |=| –e–ty+1–1| = e–ty < e.
Решая последнее неравенство, найдём t:
–ty < ln eÛ![]() Û
Û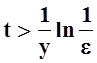 .
.
Итак, можно взять ![]() . Тогда, если t> M, то
. Тогда, если t> M, то 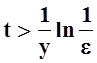 ,
а значит будет выполнено ( "yÎ[c,¥) ) неравенство | F(t,y) – I(y) | < e, что и означает
равномерную сходимость.
,
а значит будет выполнено ( "yÎ[c,¥) ) неравенство | F(t,y) – I(y) | < e, что и означает
равномерную сходимость.
Заметим, что
на множестве [0,¥)
равномерной сходимости нет. Действительно, для равномерной сходимости
требуется, чтобы "e> 0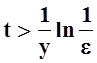 при достаточно больших t.
Однако ясно, что если e< 1,
то не существует числа t, для
которого это выполняется при любом yÎ(0, ¥).
при достаточно больших t.
Однако ясно, что если e< 1,
то не существует числа t, для
которого это выполняется при любом yÎ(0, ¥).
Доказательство равномерной сходимости несобственных интегралов удобно проводить с помощью признака Вейерштрасса – как и в случае функциональных рядов.
Теорема
7 (признак Вейерштрасса равномерной сходимости). Если для интеграла 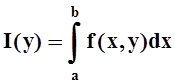 существует мажорирующий
его сходящийся интеграл
существует мажорирующий
его сходящийся интеграл 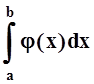 , т.е.
, т.е.
|f(x,y) |£j(x) ("xÎ[a,b), "y Î[c,d]), то I(y)сходится на [c, d] равномерно.
Доказательство не приводится. Покажем лишь применение признака Вейерштрасса на примерах.
Пример
10. Интеграл 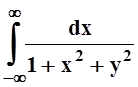 равномерно сходится на
всей оси, так как "y
равномерно сходится на
всей оси, так как "y
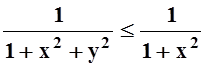 , а интеграл
, а интеграл 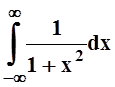 сходится:
сходится: 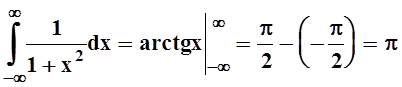 .
.
Пример
11. Интеграл 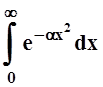 , зависящий от
параметра a,
сходится равномерно на любом промежутке [c,
¥), если c
> 0.
, зависящий от
параметра a,
сходится равномерно на любом промежутке [c,
¥), если c
> 0.
Проверим, что
мажорирующим для данного является интеграл 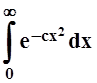 (здесь
с, в отличие от a, постоянное число). Действительно,
(здесь
с, в отличие от a, постоянное число). Действительно,
![]() ("aÎ[c, ¥)), и нужно лишь доказать, что
интеграл
("aÎ[c, ¥)), и нужно лишь доказать, что
интеграл 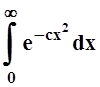 сходится. Так как
сходится. Так как 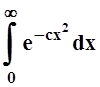
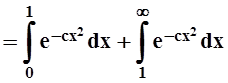 ,
то сходимость интеграла
,
то сходимость интеграла 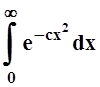 равносильна
сходимости интеграла
равносильна
сходимости интеграла 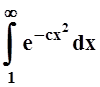 (функция
(функция ![]() непрерывна, поэтому
непрерывна, поэтому 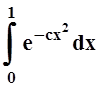 – конечное число). Для интеграла
– конечное число). Для интеграла
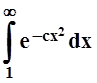 применим признак сравнения: при x ³ 1
применим признак сравнения: при x ³ 1 ![]() , а
интеграл
, а
интеграл 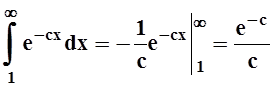 , т.е. сходится. По признаку
сравнения, сходится и
, т.е. сходится. По признаку
сравнения, сходится и 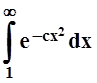 .
.
Без доказательств сформулируем теоремы о непрерывности интеграла с параметром, о дифференцировании и интегрировании по параметру, аналогичные теоремам о непрерывности суммы равномерно сходящегося функционального ряда, о почленном дифференцировании и интегрировании таких рядов.
С другой
стороны, эти теоремы похожи на соответствующие теоремы раздела 16.1, где рассматриваются собственные интегралы с параметром.
Отличие в том, что для несобственных интегралов везде требуется равномерная
сходимость. В формулировках теорем 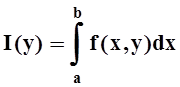 – несобственный
интеграл с особенностью в точке x = b.
– несобственный
интеграл с особенностью в точке x = b.
Теорема 8. Если функция f(x,y) непрерывна на D= [a,b) ´ [c,d], а интеграл I(y) сходится равномерно на [c, d], то I(y) – непрерывная на [c, d] функция, и "y0Î[c, d]
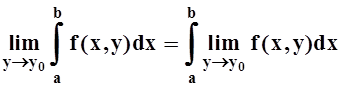 .
.
Теорема
9. Пусть f(x,y), 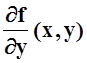 непрерывны
на D= [a,b) ´ [c,d]. Если интеграл
непрерывны
на D= [a,b) ´ [c,d]. Если интеграл 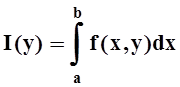 сходится в каждой точке [c,d] ,
а интеграл
сходится в каждой точке [c,d] ,
а интеграл 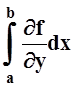 сходится равномерно на [c,d] ,
то
сходится равномерно на [c,d] ,
то
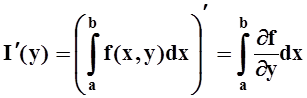 .
.
Теорема 10. Если f(x,y) непрерывна на D= [a,b) ´ [c,d] и I(y) сходится равномерно на конечном отрезке [c,d], то
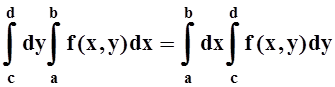 .
.
Замечание. Равномерной сходимости на бесконечном промежутке уже недостаточно – изменение порядка интегрирования в этом случае может привести к изменению результата.
16.3 Гамма–функция
Среди функций, которые не являются элементарными, одной из важнейших является так называемая гамма–функция, определяемая в виде несобственного интеграла, зависящего от параметра:
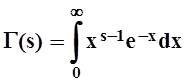 .
.
Мы рассмотрим наиболее важные свойства этой функции.
Область
определения функции Г(s)
состоит из тех чисел s,
для которых несобственный интеграл сходится. Кроме бесконечного верхнего
предела, интеграл  при s < 1
имеет ещё особенность в точке х= 0. Поэтому представим его в виде
суммы:
при s < 1
имеет ещё особенность в точке х= 0. Поэтому представим его в виде
суммы: 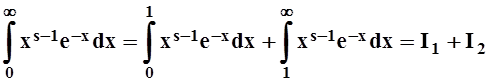 .
.
Интеграл I2 сходится при любом s. Действительно, вычислим предел (применяя, если нужно, несколько раз правило Лопиталя):
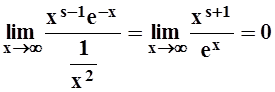 .
.
Значит, при больших х: ![]() . Но мы
знаем, что
. Но мы
знаем, что 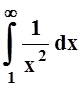 сходится. Поэтому, по признаку
сравнения,
сходится. Поэтому, по признаку
сравнения, 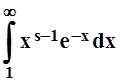 тоже сходится.
тоже сходится.
Рассмотрим
теперь  и сравним его с интегралом
и сравним его с интегралом 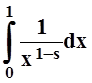 с помощью предельного признака
сравнения (теорема 3¢
из 8.2):
с помощью предельного признака
сравнения (теорема 3¢
из 8.2):
 .
.
Так как получилось конечное
ненулевое число, то либо оба интеграла сходятся, либо оба расходятся. Легко
установить (и это было сделано в 8.2), что 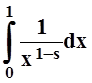 сходится
тогда и только тогда, когда 1–s
< 1, т.е. при s > 0
. Следовательно, интеграл I1
, а вместе с ним и Г(s)= I1+I2 сходятся только при s >0.
Область определения Г(s)
– все положительные действительные числа.
сходится
тогда и только тогда, когда 1–s
< 1, т.е. при s > 0
. Следовательно, интеграл I1
, а вместе с ним и Г(s)= I1+I2 сходятся только при s >0.
Область определения Г(s)
– все положительные действительные числа.
Без доказательства отметим, что функция Г(s) дифференцируема (а значит и непрерывна) в любой точке s > 0 , причём
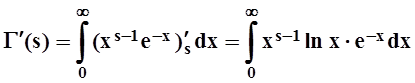 .
.
Более того, существуют производные всех порядков:
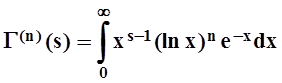 .
.
Для вывода важного свойства гамма–функции, проведём вычисления:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.