









Если известно, что поле (P,Q,R) потенциально (т.е. Pdx+Qdy+Rdz является полным дифференциалом), то его потенциал U(x,y,z) находится в точности так же, как и для плоского поля:
U(x, y, z) =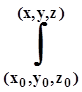 Pdx+Qdy+Rdz,
Pdx+Qdy+Rdz,
Причём интегрировать удобно по ломаной, звенья которой параллельны координатным осям.
В то же время признак полного дифференциала (теорема 4) сформулирован и доказан исключительно для плоского случая. Чтобы получить аналогичный результат для трёхмерного векторного поля, нам потребуется понятие поверхностно–односвязной области. Область в пространстве называется поверхностно–односвязной, если для любого замкнутого контура, лежащего в этой области, найдётся поверхность, ограниченная этим контуром и также целиком лежащая в области.
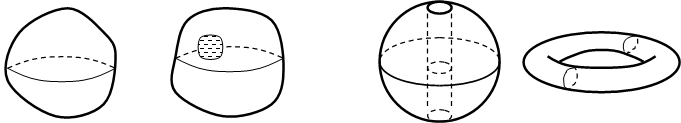 |
Поверхностно–односвязные области Области не поверхностно–односвязные
Как и в случае плоской односвязной области, можно определение дать по–другому: область в R3 является поверхностно–односвязной, если любой замкнутый контур, лежащий в ней, можно, непрерывно изменяя, стянуть в точку, оставаясь в пределах области.
Теперь сформулируем и докажем признак потенциальности векторного поля.
Теорема 6. Пусть функции P(x,y,z), Q(x,y,z), R(x,y,z) имеют непрерывные частные производные до второго порядка включительно в каждой точке поверхностно–односвязной области E. Тогда
Pdx+Qdy+Rdz – полный дифференциал Û 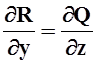 ,
, ![]() ,
, 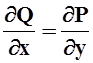 .
.
Или, на языке теории поля:
Поле ![]() =P
=P![]() +Q
+Q![]() +R
+R![]() потенциально Û rot
потенциально Û rot![]() =
=![]() .
.
Доказательство.
« Þ ». Допустим, Pdx+Qdy+Rdz =dU.
Это значит, что P=![]() , Q=
, Q=![]() , R=
, R=![]() .
Следовательно
.
Следовательно 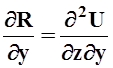 ,
, 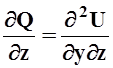 .
По теореме о равенстве смешанных частных производных, получаем:
.
По теореме о равенстве смешанных частных производных, получаем: 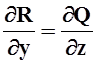 . Аналогично проверяются соотношения
. Аналогично проверяются соотношения
![]() ,
,
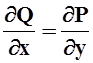 .
.
« Ü ». Пусть теперь rot![]() =
=![]() .
Возьмём любой замкнутый контур L,
лежащий в E. Рассмотрим
поверхность S,
ограниченную контуром L
и также лежащую в области E
(для существования такой поверхности и требуется, чтобы область E была
поверхностно–односвязной). Применим теорему Стокса:
.
Возьмём любой замкнутый контур L,
лежащий в E. Рассмотрим
поверхность S,
ограниченную контуром L
и также лежащую в области E
(для существования такой поверхности и требуется, чтобы область E была
поверхностно–односвязной). Применим теорему Стокса:
![]() Pdx+Qdy+Rdz=
Pdx+Qdy+Rdz=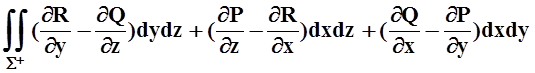 .
.
Так как rot![]() =
=![]() , то получаем, что
, то получаем, что ![]() Pdx+Qdy+Rdz= 0. Теоремы 2, 3 (справедливые, как
отмечалось, и для пространственного случая) показывают, что поле
Pdx+Qdy+Rdz= 0. Теоремы 2, 3 (справедливые, как
отмечалось, и для пространственного случая) показывают, что поле ![]() =P
=P![]() +Q
+Q![]() +R
+R![]() потенциально.
потенциально.
12.3 Обзор основных характеристик векторных полей
Мы уже познакомились с несколькими характеристиками векторного поля – циркуляцией, потоком, ротором. Рассмотрим здесь ещё одну величину – дивергенцию.
Пусть ![]() векторное поле в некоторой
пространственной области. Пусть S – замкнутая поверхность, E – часть пространства, ограниченная
поверхностью S.
Рассмотрим поток поля
векторное поле в некоторой
пространственной области. Пусть S – замкнутая поверхность, E – часть пространства, ограниченная
поверхностью S.
Рассмотрим поток поля ![]() через поверхность S:
через поверхность S:
P= ![]() (
(![]() ,
, ![]() ) ds.
) ds.
 Здесь
Здесь ![]() –
единичный вектор внешней нормали к поверхности. Чтобы лучше понять дальнейшие
рассуждения, будем считать, что
–
единичный вектор внешней нормали к поверхности. Чтобы лучше понять дальнейшие
рассуждения, будем считать, что ![]() – поле скоростей
частиц жидкости. Если поток через замкнутую поверхность S больше нуля, можно
представить, что жидкость «возникает» в некоторых точках E, имеются «источники». Если же поток
меньше нуля, то в некоторых точках E
жидкость «исчезает», имеются «стоки». Считая, что в области E имеются как «источники», так и
«стоки», можно интерпретировать поток P как суммарную мощность
«источников» и «стоков» (мощность «стоков» считается отрицательной).
– поле скоростей
частиц жидкости. Если поток через замкнутую поверхность S больше нуля, можно
представить, что жидкость «возникает» в некоторых точках E, имеются «источники». Если же поток
меньше нуля, то в некоторых точках E
жидкость «исчезает», имеются «стоки». Считая, что в области E имеются как «источники», так и
«стоки», можно интерпретировать поток P как суммарную мощность
«источников» и «стоков» (мощность «стоков» считается отрицательной).
Пусть V(E)
– объём области E.
Тогда отношение ![]() естественно назвать
средней мощностью (или плотностью) «источников» и «стоков» в
области E.
естественно назвать
средней мощностью (или плотностью) «источников» и «стоков» в
области E.
Пусть M – какая–либо точка E. Вычисляя плотность
«источников» и «стоков» во всё меньших окрестностях точки M, можно перейти к пределу при E®M (при этом V(E)
® 0, конечно). Мы получим плотность
«источников» и «стоков» в точке M.
Эта величина называется дивергенцией
поля ![]() в точке M:
в точке M:
div![]() =
=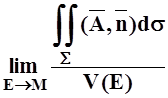 .
.
Теорема
7. Если ![]() =P
=P![]() +Q
+Q![]() +R
+R![]() ,
причём функции P, Q, R непрерывны и имеют непрерывные частные
производные 1–го порядка, то в любой точке
,
причём функции P, Q, R непрерывны и имеют непрерывные частные
производные 1–го порядка, то в любой точке
div![]() =
= 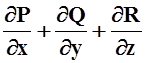 .
.
Доказательство. Пусть M0 – произвольная точка, E – какая–либо область, содержащая M0, S – поверхность, ограничивающая E. По теореме Гаусса – Остроградского
![]() (
(![]() ,
, ![]() ) ds =
) ds = 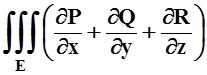 dxdydz.
dxdydz.
Воспользуемся теоремой о среднем для тройного интеграла
![]() (
(![]() ,
, ![]() ) ds =
) ds =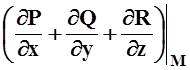 × V(E).
× V(E).
Здесь M – некоторая точка в E, V(E) – объём E. Перейдём к пределу при E®M0, учитывая, что при этом
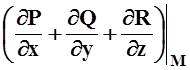 ®
® 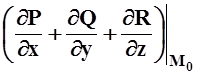
следует из непрерывности частных производных). Получим
div![]() (M0) =
(M0) =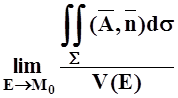 =
= 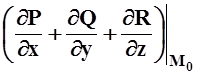 , что и требовалось доказать.
, что и требовалось доказать.
Заметим, что
представление поля ![]() в виде
в виде ![]() =P
=P![]() +Q
+Q![]() +R
+R![]() зависит
от выбора системы координат. При изменении системы координат то же самое поле
зависит
от выбора системы координат. При изменении системы координат то же самое поле ![]() будет задаваться другими функциями P, Q, R.
будет задаваться другими функциями P, Q, R.
Мы могли бы
дать более простое определение дивергенции, сразу называя дивергенцией величину
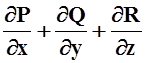 .
Однако тогда было бы неясно – зависит ли дивергенция от системы координат?
Определение дивергенции с помощью предела (т.е. как «плотности источников и
стоков») инвариантно относительно выбора системы координат.
.
Однако тогда было бы неясно – зависит ли дивергенция от системы координат?
Определение дивергенции с помощью предела (т.е. как «плотности источников и
стоков») инвариантно относительно выбора системы координат.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.