Можно доказать, что ротор, как и дивергенция, тоже является характеристикой самого поля и не зависит от системы координат (хотя в данном выше определении ротора участвуют функции P, Q, R). Независимость от системы координат циркуляции и потока следует сразу из определений, если записать подинтегральные выражения через скалярное произведение:
циркуляция: 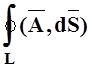 ; поток:
; поток: ![]() (
(![]() ,
, ![]() ) ds.
) ds.
Мы подробно
рассмотрели свойства векторного поля, у которого rot![]() =
=![]() в каждой точке – это потенциальное
поле. Теперь пусть векторное поле
в каждой точке – это потенциальное
поле. Теперь пусть векторное поле ![]() таково,
что div
таково,
что div![]() = 0 в каждой
точке. Такое поле называется соленоидальным,
или трубчатым. Ясно, что соленоидальное поле не имеет ни «источников», ни
«стоков». Поток такого поля через любую замкнутую поверхность равен нулю.
= 0 в каждой
точке. Такое поле называется соленоидальным,
или трубчатым. Ясно, что соленоидальное поле не имеет ни «источников», ни
«стоков». Поток такого поля через любую замкнутую поверхность равен нулю.
Если ![]() – произвольное векторное поле, то rot
– произвольное векторное поле, то rot![]() – соленоидальное
поле. Действительно,
– соленоидальное
поле. Действительно,
div (rot![]() ) =
) = 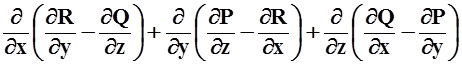 = 0.
= 0.
Оказывается, справедливо и обратное: любое соленоидальное поле является полем ротора. Итак, можно доказать, что
![]() – соленоидально Û $
– соленоидально Û $![]() :
: ![]() =rot
=rot![]() .
.
Укажем (также без доказательства), что любое векторное поле можно представить в виде суммы потенциального и соленоидального полей:
" ![]() $
$![]() – потенциальное,
$
– потенциальное,
$![]() – соленоидальное:
– соленоидальное:
![]() =
=![]() +
+![]() .
.
Наконец,
возможен случай, когда поле является одновременно и
потенциальным, и соленоидальным. Такие векторные поля называются гармоническими,
их изучение связано с изучением гармонических функций. Функция U=U(x,y,z) называется гармонической,
если 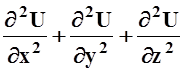 = 0.
= 0.
Теорема
8. Векторное поле ![]() – гармоническое Û его потенциал –
гармоническая функция.
– гармоническое Û его потенциал –
гармоническая функция.
Доказательство.
Пусть U – потенциал ![]() , т.е.
, т.е. ![]() =gradU==
=gradU==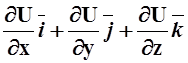 .
Тогда:
.
Тогда: ![]() – гармоническое Û
– гармоническое Û
Û div![]() = 0 Û
= 0 Û
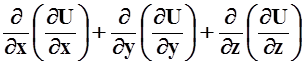 = 0 Û
= 0 Û 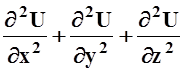 = 0.
= 0.
В заключение раздела рассмотрим удобный для работы с векторными полями способ записи – с помощью символического оператора Гамильтона
Ñ=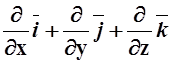 .
.
Знак Ñ читается «набла». Оператор «набла» можно «умножать» на скалярную функцию (вычисляя от неё частные производные), «умножать» скалярно и векторно на векторную функцию по обычным правилам векторной алгебры.
Используя оператор Гамильтона, приведём краткую и удобную запись для основных характеристик скалярных и векторных полей:
ÑU =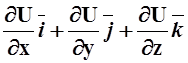 =
grad U;
=
grad U;
(Ñ, ![]() ) =(
) =(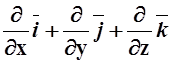 , P
, P![]() + Q
+ Q![]() + R
+ R![]() )
=
)
=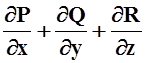 = div
= div ![]() ;
;
[Ñ, ![]() ] =
] =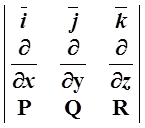 =rot
=rot![]() .
.
Применяя оператор «набла» повторно, можно вычислять и более сложные величины:
(Ñ, ÑU) = div (grad U),
[Ñ, ÑU] = rot (grad U),
Ñ×(Ñ, ![]() ) = grad (div
) = grad (div ![]() ),
),
(Ñ,[Ñ, ![]() ]) = div
(rot
]) = div
(rot ![]() ),
),
[Ñ,[Ñ, ![]() ]] = rot
(rot
]] = rot
(rot ![]() ).
).
Впрочем, как мы уже знаем, всегда
rot (grad U) =![]() , div
(rot
, div
(rot ![]() ) = 0.
) = 0.
Скалярный квадрат оператора Ñ называется оператором Лапласа D:
D= (Ñ,Ñ) =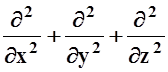 .
.
Гармонические функции, с которыми мы уже встречались, можно определить как функции, удовлетворяющие уравнению Лапласа: DU= 0.
12.4 Задачи с решениями
1.
Найти циркуляцию векторного поля ![]() = (x–y–z)
= (x–y–z)![]() + 3z
+ 3z![]() + (2x–y)
+ (2x–y)![]()
вдоль линии L пересечения поверхностей 4z=x2+ 4y2, z= 1. Направление обхода – против часовой стрелки, если смотреть из точки (0, 0, 2).
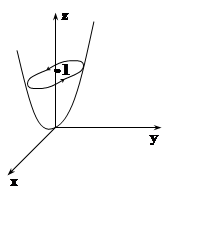 Решение.
Линия пересечения – эллипс, лежащий в плоскости z= 1. Его уравнение имеет вид: 4 =x2+ 4y2,
z= 1. Или:
Решение.
Линия пересечения – эллипс, лежащий в плоскости z= 1. Его уравнение имеет вид: 4 =x2+ 4y2,
z= 1. Или: ![]() +y2= 1, z= 1.
Зададим этот эллипс параметрически:
+y2= 1, z= 1.
Зададим этот эллипс параметрически:
x = 2cos t, y = sin t, z = 1; t Î [0, 2p].
Циркуляцию вычисляем, сводя криволинейный интеграл к интегралу по параметру t:
![]() (x–y–z)dx+ 3zdy+ (2x–y)dz=
(x–y–z)dx+ 3zdy+ (2x–y)dz=
= ![]() [(2cos t – sin t – 1) (– 2sin t) + 3cos t + 0]dt =
[(2cos t – sin t – 1) (– 2sin t) + 3cos t + 0]dt =
= ![]() (– 4cos t sin t + 2sin2t + 2sin t +
3cos t) dt =
(– 4cos t sin t + 2sin2t + 2sin t +
3cos t) dt =
=– 4![]() sin t d(sin t) + 2
sin t d(sin t) + 2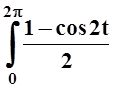 dt
– 2cos t
dt
– 2cos t![]() + 3sin t
+ 3sin t![]() =
=
=– 4 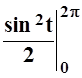 + (t–
+ (t–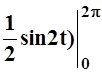 = 2p.
= 2p.
2. Найти функцию U(x, y),
если известен её дифференциал: dU=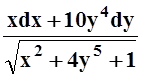 .
.
Решение. Доказывая теорему 2, мы видели, что U(x, y) можно найти по формуле:
U(x, y) = ![]() dU.
dU.
Начальная точка может быть произвольной – функция U(x, y) определяется с точностью до постоянного слагаемого. Интегрировать можно по любому пути, так как интеграл от полного дифференциала не зависит от пути.
Возьмём в качестве начальной точки (0, 0), интегрировать будем по ломаной.
U(x, y) =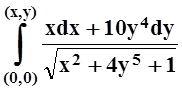 =
= 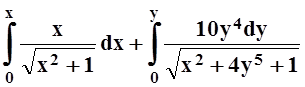 =
=
= 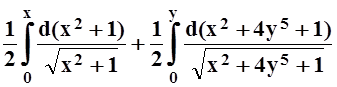 =
=![]() =
=
=![]() – 1 +
– 1 + ![]() –
– ![]() =
= ![]() +C.
+C.
3. Проверить, что поле
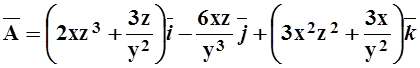
является потенциальным и найти его потенциал.
Решение. Для проверки потенциальности поля вычислим его ротор:
rot![]() =
=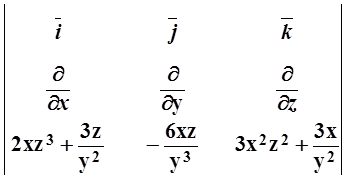 =
=
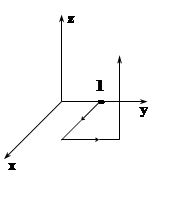 =
=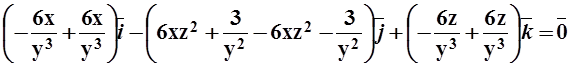 .
.
Значит, поле потенциально. Найдём потенциал по формуле
U(x, y, z) =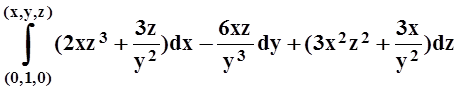 .
.
Интегрируем по ломаной:
U(x, y, z) =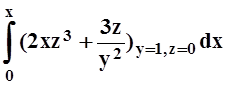 –
– 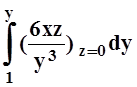 +
+
+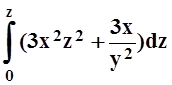 =x2z3+
=x2z3+![]() +C.
+C.
4. Вычислить поверхностный интеграл
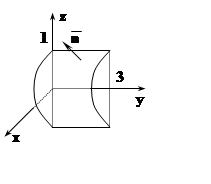
![]() ydxdz+ (1 +xz)dydz, где S¢–
верхняя сторона части цилиндрической поверхности
ydxdz+ (1 +xz)dydz, где S¢–
верхняя сторона части цилиндрической поверхности
x2 + z2 = 1, x ³ 0, 0 £ y £ 3.
Решение.
Сделаем чертёж. Поверхность удобно проецировать на плоскость YOZ, поэтому будем вычислять
интеграл, сводя его к двойному интегралу по переменным y, z. Уравнение S: ![]() ; элемент
поверхности:
; элемент
поверхности: ![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.