Дифференцирование функций нескольких переменных

Доказательство. Так как E связно, то существует непрерывная кривая, соединяющая точки  A, B  и лежащая в  E  (см. 9.1.4). Подробнее, это значит, что существуют непрерывные функции  x₁= j₁(t),..., x_n= j_n(t),  определённые на некотором отрезке  [a,b]   такие, что

"t Î[a,b]     P(t) = ( j₁(t),j₂(t),...,j_n(t) )ÎE,

P(a) = A,        P(b) = B.

Рассмотрим сложную функцию

f(P(t)) = f( j₁(t),j₂(t),...,j_n(t) ).

По теореме 8 она непрерывна. Кроме того, f(P(a)) £ k £ f(P(b)). По теореме о промежуточных значениях для функций одной переменной (теорема 3 из 3.2), существует gÎ[a,b]:  f(P(g)) = k.  Ясно, что C = P(g) = ( j₁(g),j₂(g),...,j_n(g) ) – искомая точка.

Определение равномерно непрерывной на множестве  DÍRⁿ  функции полностью аналогично определению равномерно непрерывной функции одной переменной (см. 3.5):

  f  равномерно непрерывна на  D    Û

Û"e>0  $d>0 :"P,P¢ÎD   | P–P¢| < dÞ| f(P) – f(P¢) | < e.

Аналогична теореме 12 из 3.5 и следующая теорема, которую здесь мы приводим без доказательства.

Теорема 11 (теорема Кантора). Непрерывная на компактном множестве функция равномерно непрерывна.

9.4 Дифференцирование функций нескольких переменных

9.4.1  Частные производные. Для сокращения записи рассмотрим случай функции двух переменных:

f : D®R,    DÍR².

Пусть  P_o(x_o, y_o)ÎD.  Дадим приращение   переменной  х, оставляя  y = y₀  без изменения. Тогда разность

называется  частным приращением  по переменной х функции f в точке P_o. Если существует конечный предел

то он называется частной производной функции f по переменной х в точке P_o. Используются обозначения

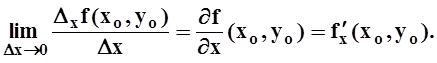
Аналогично определяется частная производная по переменной y:

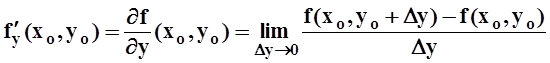
Таким образом, частная производная функции в данной точке – это число. Если же точку не фиксировать, а менять, то частные производные 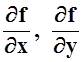   снова являются  функциями переменных   x,  y.

В случае, если функция f зависит от большего числа переменных, определение частной производной аналогично: это обычная производная по одной из переменных, вычисленная в предположении, что все остальные переменные зафиксированы. Отсюда следует, что вычислять частную производную по какой–либо переменной нужно по обычным правилам дифференцирования, рассматривая все остальные переменные как постоянные.

Пример 6.  Найти частные производные функции     .

Решение.Дифференцируя по  х,  считаем   y  и  z   постоянными:

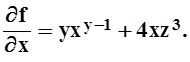     Аналогично: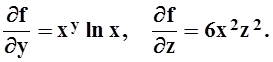       

Замечание. Из существования частных производных ещё не следует непрерывность функции.   Рассмотрим функцию      .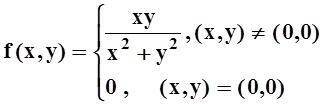

Так как 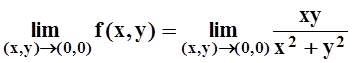   не существует  (см. пример 4), то  f(x,y) не является непрерывной в точке  (0,0). Однако частные производные существуют в любой точке плоскости. Действительно,

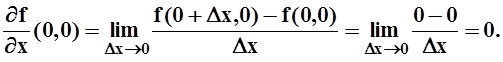
Аналогично, 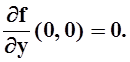  Во всех остальных точках частные производные вычисляются по обычным правилам:

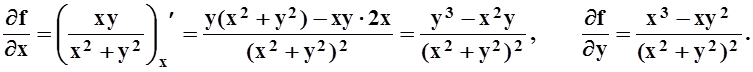
9.4.2  Дифференцируемость функции. Понятие дифференциала.Мы опять будем рассматривать функции 2–х переменных. Общий случай полностью аналогичен, но требует более громоздких записей.

Пусть функция  f(x, y)  определена в окрестности точки  (x_o, y_o).  Дадим приращения   переменным  x, y.   Тогда разность

называется  полным приращением  функции в точке  (x_o, y_o).

Теорема 12 . Если частные производны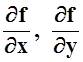е  существуют и непрерывны в некоторой окрестности точки  (x_o, y_o), то полное приращение функции можно представить в виде:

где 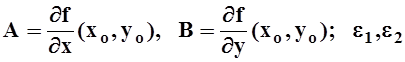  – функции от  причём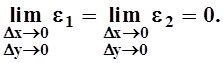

Доказательство.  Запишем   в следующем виде:

.

Применим к каждой разности теорему Лагранжа (теорема 4 из 5.1). Подробнее: можно считать, что в первой скобке функция одной переменной    имеет в каждой точке отрезка    производную, поэтому  :

.

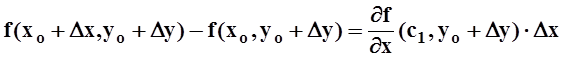Аналогично для второй скобки: :

.

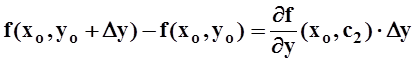Итак,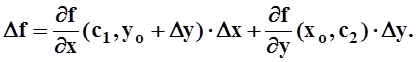  

Воспользуемся непрерывностью частных производных: так как при , то 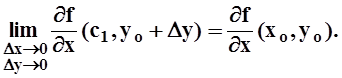  Отсюда следует, что функция  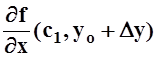  отличается от числа  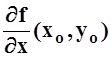  на функцию   предел которой  (при  )  равен  0 (т.е.  на   бесконечно  малую):

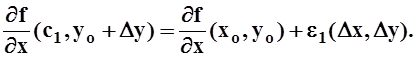
Аналогично,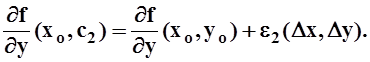  

Подставим полученные формулы в выражение для  :

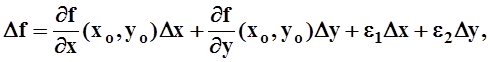
что и требовалось доказать.

Функция  f(x,y),  для которой выполнены условия  (а значит и заключение) теоремы 12,  называется  дифференцируемойв точке  (x_o,y_o).  Выражение

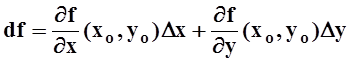
называется  дифференциалом(полным дифференциалом) функции  f(x,y)в точке (x_o,y_o).

Замечание. Если  f(x,y) дифференцируема в точке  (x_o,y_o),  то она непрерывна в этой точке.  Действительно,

.

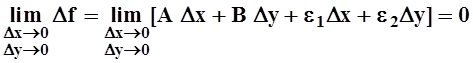Так как  то это равносильно тому, что 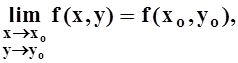  т.е. непрерывности функции  f(x, y)в точке  (x_o, y_o).

Обратим внимание: дифференциал  df  является линейной функцией  от приращений   в то время, как приращение   может зависеть от    очень сложно. С другой стороны, разность   не только стремится к 0 при   но и является, как говорят, бесконечно малой более высокого порядка, по сравнению с  «модулем полного приращения переменных» :

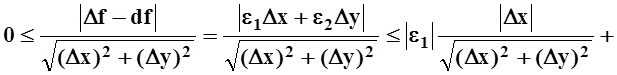
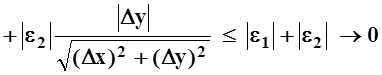  (при  ).

Иногда это обстоятельство записывают в виде приближённого равенства:  и называют дифференциал  главной,  линейной частью приращения.

Пример 7.  Как изменится объём конуса с высотой 60 см, радиусом основания 20 см, если высоту увеличить на 3 мм, а радиус уменьшить на 1 мм?

Решение. Объём конуса – этой функция от высоты H и радиуса основания      В задаче требуется найти приращение функции

Проще это сделать приближённо, с помощью дифференциала

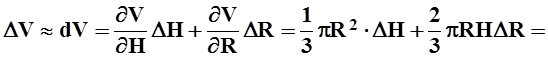
 – 126 (см³).

Объём конуса уменьшится приблизительнона 126 см³. Здесь мы не будем оценивать допущенную нами ошибку, укажем только, что она составляет около 1 см³ .

Дифференциал   df   часто записывают в виде

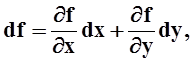
учитывая, что для независимых переменных    

В общем случае, для функции  n  переменных  f(x₁, x₂, …, x_n)

.

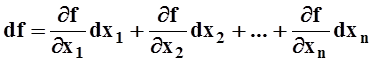Рассмотрим правило дифференцирования сложных функций нескольких переменных.