Заметим, что смешанные частные
производные 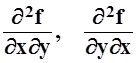 оказались одинаковыми. Это
не совпадение, справедлива общая теорема, которую мы приводим без
доказательства.
оказались одинаковыми. Это
не совпадение, справедлива общая теорема, которую мы приводим без
доказательства.
Теорема 14.Если частные производные k–го порядка функции f непрерывны, то смешанные частные производные, отличающиеся лишь порядком дифференцирования, равны.
Познакомимся
теперь с понятием дифференциала 2–го и более высоких порядков. Пока мы
рассматривали дифференциал 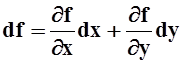 в данной точке
как линейную функцию от приращений. Другими словами,
в данной точке
как линейную функцию от приращений. Другими словами, 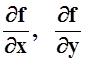 –
числа (значения частных производных в данной точке), dx, dy – переменные приращения.
–
числа (значения частных производных в данной точке), dx, dy – переменные приращения.
Теперь поступим по–другому. Зафиксируем приращения dx, dy, а точку, где вычисляется df, будем менять. Тогда дифференциал df является снова функцией от x, y. Дифференциал этой функции называется дифференциалом второго порядка (или вторым дифференциалом):
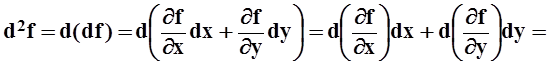
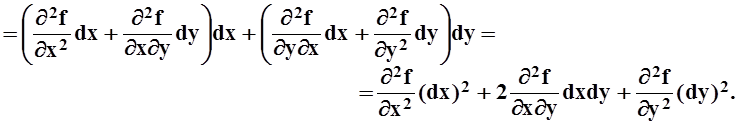
Мы воспользовались тем, что, по теореме 14, 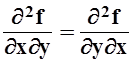 .
.
Если d2f вычисляется в некоторой точке, то частные производные принимают числовые значения, d2f является функцией от приращений. А точнее – второй дифференциал является квадратичной формой от приращений dx, dy.
Если же приращения dx, dy зафиксировать, а менять точку, то можно перейти к дифференциалу 3–го порядка:
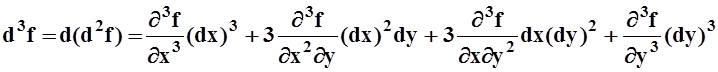 .
.
С помощью индукции можно получить формулу для дифференциала n–го порядка для функции двух переменных:
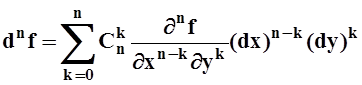 , здесь
, здесь ![]() – биномиальные
коэффициенты.
– биномиальные
коэффициенты.
Пример 10.Найти дифференциал 2–го порядка функции f(x, y)= x2y3–2y2 в точке P(2, 1).
Решение. 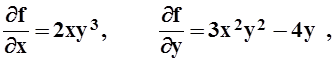
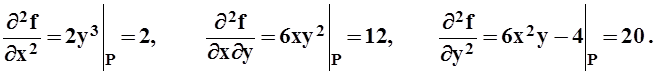
Следовательно,
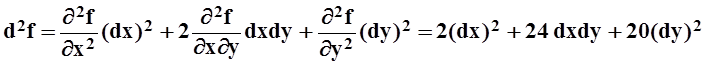 .
.
9.5 Задачи с решениями
1.Найти и изобразить область D определения функции 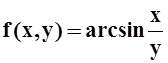 . Является ли D открытым или замкнутым множеством?
. Является ли D открытым или замкнутым множеством?
Решение.Так как арксинус определён на отрезке [–1, 1],
то в область определения функции f входят те точки, для которых 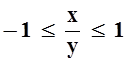 . Для упрощения неравенства нужно
рассмотреть 2 случая.
. Для упрощения неравенства нужно
рассмотреть 2 случая.
1) 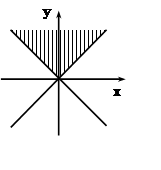 Найдём
точки, для которыхy> 0.
Умножая все части неравенства на y,
получим: –y£x£y. Рассмотрим одно из неравенств: x£y. Заменим знак £ на знак =.
Найдём
точки, для которыхy> 0.
Умножая все части неравенства на y,
получим: –y£x£y. Рассмотрим одно из неравенств: x£y. Заменим знак £ на знак =. 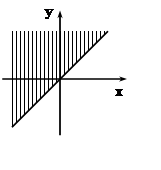 Уравнение x= yопределяет прямую линию, разделяющую
плоскость на 2 полуплоскости. Одна из них (на рисунке заштрихована)
состоит из точек с условием x<y, другая
– из точек, для которых x>y.
Значит { (x, y) | x£y}
– отмеченная на рисунке полуплоскость, включающая ограничивающую её
прямую. Аналогично находим полуплоскость {
(x, y)
| –y£x}.
Так как должны быть выполнены оба неравенства, то следует взять пересечение
этих полуплоскостей. Условие y>
0 показывает, что точка (0,0) не должна включаться в найденную
область.
Уравнение x= yопределяет прямую линию, разделяющую
плоскость на 2 полуплоскости. Одна из них (на рисунке заштрихована)
состоит из точек с условием x<y, другая
– из точек, для которых x>y.
Значит { (x, y) | x£y}
– отмеченная на рисунке полуплоскость, включающая ограничивающую её
прямую. Аналогично находим полуплоскость {
(x, y)
| –y£x}.
Так как должны быть выполнены оба неравенства, то следует взять пересечение
этих полуплоскостей. Условие y>
0 показывает, что точка (0,0) не должна включаться в найденную
область.
2) Найдём точки, для которых y< 0:
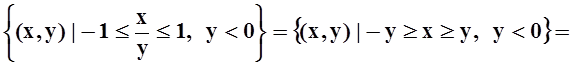
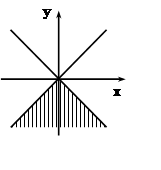
![]() .
.
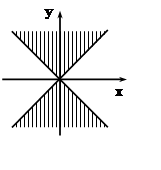 Аналогично первому случаю,
находим нужное множество. Рассматривая объединение полученных множеств, находим
искомую область определения D.
Точка (0,0) в область определения не входит, хотя и
является для неё граничной. Значит,D – не является замкнутым
множеством.
Аналогично первому случаю,
находим нужное множество. Рассматривая объединение полученных множеств, находим
искомую область определения D.
Точка (0,0) в область определения не входит, хотя и
является для неё граничной. Значит,D – не является замкнутым
множеством.
Остальные граничные точки – точки прямых y= x, y= –x – входят в D, поэтому D не является и открытым множеством. Заметим также, что D не является ни ограниченным, ни связным множеством.
2. Вычислить
предел 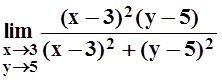 , или доказать, что он не существует.
, или доказать, что он не существует.
Решение.Разделим числитель и знаменатель на (x–3)2:
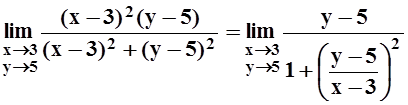 .
.
Числитель стремится к 0,
знаменатель не может быть меньше 1,
функция 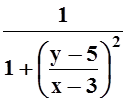 ограничена. Произведение бесконечно
малой функции на ограниченную стремится к 0.
Следовательно, предел равен 0.
ограничена. Произведение бесконечно
малой функции на ограниченную стремится к 0.
Следовательно, предел равен 0.
3. Исследовать на непрерывность функцию
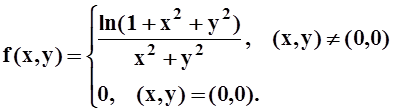
Решение.Во всех точках, кроме (0,0), функция непрерывна – по теоремам об арифметических свойствах непрерывных функций и о непрерывности сложной функции. Чтобы проверить непрерывность в точке (0,0), вычислим предел:
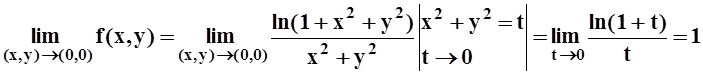 .
.
Предел не равен значению: f(0,0) = 0, поэтому функция имеет в точке (0,0) разрыв.
4. Найти все частные производные 1 и 2 порядков функции z= ln(2x+siny).
Решение.Найдём сначала частные производные 1–го порядка. Дифференцируя по одной из переменных, другую рассматриваем как постоянную.
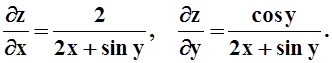
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.