Дифференцируя повторно, находим частные производные 2–го порядка:
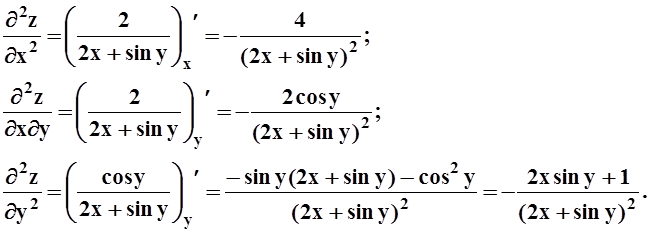
5. Найти
дифференциал 2–го порядка функции z= 5x2y–
3sinx+
2cosy в точке 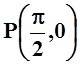 .
.
Решение. 1 способ – вычисляя частные производные. Находим все частные производные 2–го порядка:
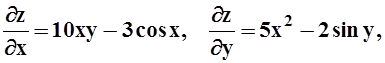
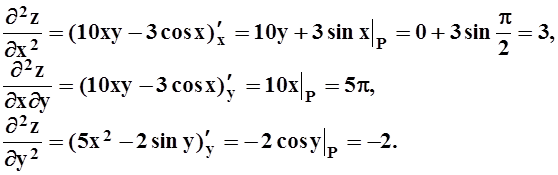
Подставляем в формулу дифференциала 2–го порядка:
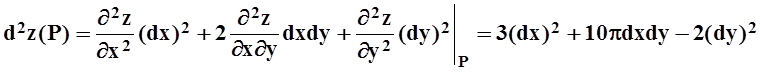 .
.
2 способ – используя правила вычисления дифференциалов. Сначала вычисляем дифференциал 1–го порядка:
dz= d(5x2y–3sinx+2cosy) = 5d(x2y)–3d(sinx)+2d(cosy) =
= 5(yd(x2)+x2dy)–3cosxdx–2sinydy= 10xydx+5x2dy–3cosxdx–2sinydy.
Теперь вычисляем d2z, считая dx, dy постоянными:
d2z= d(dz) = 10d(xy)dx+5d(x2)dy–3d(cosx)dx–d(2siny)dy=
= 10y(dx)2+10xdxdy+10xdxdy+3sinx(dx)2–2cosy(dy)2 =
= (10y+3sinx)(dx)2+20xdxdy–2cosy(dy)2.
Подставляя координаты точки, получим ответ:
d2z(P) = 3(dx)2+10pdxdy–2(dy)2.
6. Вычислить
приближённо 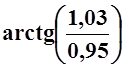 .
.
Решение.Рассмотрим функцию 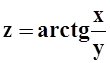 . В точке x0=1, y0=1 значение функции
легко вычисляется:
. В точке x0=1, y0=1 значение функции
легко вычисляется: ![]() . Найдём с помощью
дифференциала приращение функции, соответствующее приращениям dx=0,03, dy=–0,05:
. Найдём с помощью
дифференциала приращение функции, соответствующее приращениям dx=0,03, dy=–0,05:
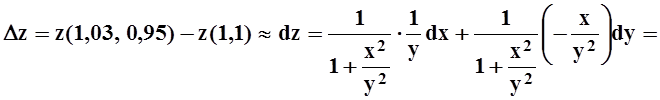
![]() .
.
Следовательно
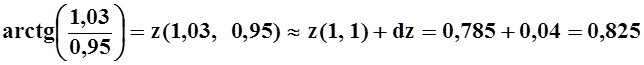 .
.
9.6 Упражнения для самостоятельной работы
1. Найти и изобразить область определения функции. Является ли она открытым или замкнутым множеством?
а) ![]() ;
б) z= ln(y2–
8x);
;
б) z= ln(y2–
8x);
в) 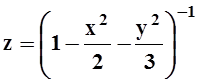 ;
г)
;
г) ![]() ;
;
д) 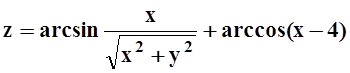 ; е)
; е) ![]() ;
;
ж) 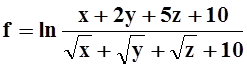 ;
з)
;
з) 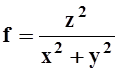 .
.
2. Вычислить предел или доказать, что он не существует:
а) 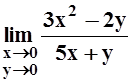 ; б)
; б)
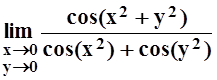 ;
;
в) 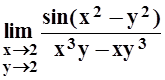 ; г)
; г)
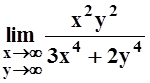 ;
;
д) 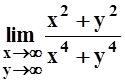 ; е)
; е)
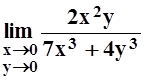 ;
;
ж) 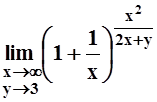 ;
з)
;
з) 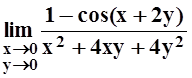 .
.
3. Исследовать функции на непрерывность:
а) z= ln(x2+2y);
б) 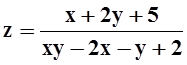 ;
;
в) 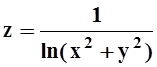 ;
г)
;
г) ![]() ;
;
д) 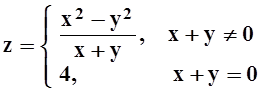 ; е)
; е)
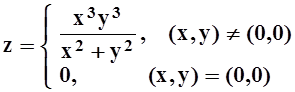 .
.
4. Найти частные производные 1–го порядка следующих функций:
а) ![]() ; б)
; б)
![]() ;
;
в) 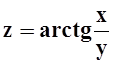 ;
г) z= (2x+3y)
sin(2x+y);
;
г) z= (2x+3y)
sin(2x+y);
д) 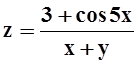 ;
е)
;
е) 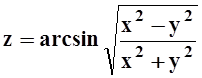 ;
;
ж) f= (x+2z)y ;
з) 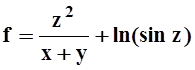 .
.
5. Найти значения всех частных производных 2–го порядка следующих функций в данной точке P.
а)z= x3+2y3–5x2y2, P(5,
1); б) 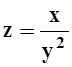 , P(4,
2);
, P(4,
2);
в) ![]() , P(0,
1); г)
, P(0,
1); г) 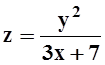 , P(–2, 1).
, P(–2, 1).
6. Найти указанные частные производные для данных функций.
а) z= x3lny+y3lnx, 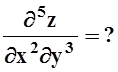 б) z= y2(3x2+y+5xy2),
б) z= y2(3x2+y+5xy2),
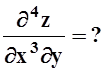
в) z= xsin(x+y), 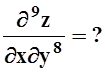 г)
f= exyz,
г)
f= exyz, 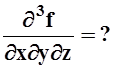
7. Найти дифференциалы 1 и 2 порядков следующих функций:
а)z= ln(x–y); б)z= xarctgy;
в) z= 5xy; г) f= xy+xz+yz.
8. Найти дифференциалы 1 и 2 порядков следующих функций в указанной точке P.
а) z= x3+2x2y+3xy2+4y3,
P(2, 1);
б) 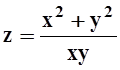 , P(2,
2);
, P(2,
2);
в) ![]() ,
, 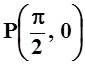 ; г)
; г) ![]() , P(1,
1, 1).
, P(1,
1, 1).
9. Вычислить
приближённо, заменяя полное приращение соответствующей функции её
дифференциалом 1–го порядка. Считать p» 3,14; ln2 » 0,69;
![]() .
.
а) 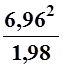 ; б) ln(3,992+2,034);
в) 2,012,94; г)
; б) ln(3,992+2,034);
в) 2,012,94; г)
![]() ; д) cos59o×tg46o; е)
; д) cos59o×tg46o; е) 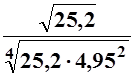 .
.
9.7 Образец теста
(для дистанционной формы обучения).
1. Область
определения функции 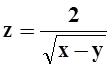 является 1) ограниченным
множеством; 2) открытым множеством; 3) замкнутым множеством; 4) не является
множеством ни одного из указанных типов.
является 1) ограниченным
множеством; 2) открытым множеством; 3) замкнутым множеством; 4) не является
множеством ни одного из указанных типов.
Указать номер правильного ответа.
2. Вычислить 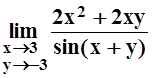 .
.
3. При каком
C функция 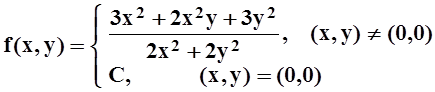 будет непрерывной на всей плоскости?
будет непрерывной на всей плоскости?
4. Найти
значение частной производной по переменной y функции
z= = ln(cos(x2y))
в точке 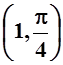 .
.
5. Найти
значение 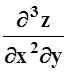 в точке (1, 5) , если
z= (x+y) arctgx.
в точке (1, 5) , если
z= (x+y) arctgx.
6. Вычислить
значение дифференциала 1–го порядка функции ![]() в
точке (5, 2), если приращения переменных известны: dx= 0,2,
dy= 0,1.
в
точке (5, 2), если приращения переменных известны: dx= 0,2,
dy= 0,1.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.