МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ
ФЕДЕРАЦИИ
МОСКОВСКИЙ АВИАЦИОННЫЙ ИНСТИТУТ
(ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ)
«МАИ»
Учебное подразделение МАИ
«Обучение студентов в г. Серпухове»
МЕТРОЛОГИЯ И РАДИОИЗМЕРЕНИЯ
Обработка результатов измерений
Учебно-методическое пособие к расчетно-графической работе
студентов, обучающихся по специальности
«Комплексная защита объектов информатизации»
|
СЕРПУХОВ – 2007
ББК 31.2
Учебно-методическое пособие предназначено студентам Московского авиационного института (Государственного технического университета), обучающимся по специальности «Комплексная защита объектов информатизации», для выполнения расчетно-графической работы по учебной дисциплине «Метрология и радиоизмерения». Оно содержит краткие теоретические сведения обработки результатов измерений, примеры решения задач, порядок выбора индивидуального варианта и рекомендации по решению и оформлению результатов расчетно-графической работы.
Рецензент: заместитель заведующего кафедрой Информатики и информационных технологий учебного подразделения МАИ
к.т.н., доцент
Введение
Разработка, изготовление и эксплуатация радиоэлектронных и электронно-вычислительных средств, используемых в технических системах и каналах передачи информации, неизбежно связаны с выполнением большого объема многочисленных измерений. При этом получаемая измерительная информация используется как для собственно измерительных целей, так и для выработки управляющих сигналов в технических системах и каналах передачи информации, а также для комплексной защиты объектов информатизации.
Поэтому перед специалистом появляется задача правильного выбора метода и средств измерений, совершенной организации измерительного эксперимента, обработки и представлений результатов измерений в соответствии с принципами метрологии и действующими в этой области как отечественными, так и международными нормативными документами.
В учебно-методическом пособии предлагается обучаемым решить пять контрольных задач расчетно-графической работы, связанных с выбором средств электрических измерений и обработкой как однократных, так и многократных измерений электрических величин.
Результаты решения расчетно-графической работы следует представить в виде пояснительной записки формата А4 (297х210 мм) или в электронном виде, примеры оформления которой приведены в приложении В к данному учебно-методическому пособию.
1. Краткие сведения из теории и примеры решения задач
Результат измерения – это математическое выражение, определяющее область нахождения истинного значения. Наиболее часто это математическое выражение записывают в форме
А = (АИЗМ ± Δ)D, P = Pд, (1)
где А – обозначение измеряемой величины;
АИЗМ - измеренное значение величины;
Δ ─ предельное значение допускаемой абсолютной погрешности;
D─ размерность измеряемой величины;
P = Pд ─ значение доверительной вероятности.
При однократных измерениях предельное значение допускаемой абсолютной погрешности Δ определяется по формуле
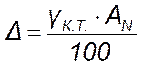 , (2)
, (2)
где γК.Т. – класс точности, значение которого на шкале измерительного прибора не подчеркнуто ломанной линией (для измерительных средств с равномерными шкалами);
АN – нормирующее значение, которое определяется следующим образом.
Если шкала равномерная и несимметричная, как прямая, так и обратная, и имеет нулевую отметку, то максимальное оцифрованное значение шкалы есть нормирующее значение АN = АМАХ.
Если шкала равномерная и симметричная относительно нулевой отметки, то нормирующее значение определяется как арифметическая сумма максимальных оцифрованных значений шкалы слева и справа от нулевого значения АN = АМАХ слева + АМАХ справа.
Если шкала равномерная и симметричная относительно номинального ненулевого значения, то это номинальное ненулевое значение, например, 50 Гц, является нормирующим значением АN = АNOM ;
Если шкала равномерная и несимметричная, не имеет нулевой отметки, например, медицинский термометр, то нормирующее значение определяется как разность между максимальным и минимальным оцифрованными значениями АN = AMAX – AMIN.
Для существенно
неравномерных шкал, на которых цифровое обозначение класса точности подчеркнуто
ломанной линией, предельное значение допускаемой абсолютной погрешности Δ (2)
определяется по формуле где 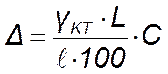 , (3)
, (3)
![]() γКТ –
класс точности измерительного прибора, указанный на шкале в виде цифры над
знаком ломанной линии ;
γКТ –
класс точности измерительного прибора, указанный на шкале в виде цифры над
знаком ломанной линии ;
L – длина рабочей части шкалы мегаомметра (указана в паспорте прибора), мм;
ℓ - длина участка шкалы между соседними оцифрованными делениями, где остановилась указательная стрелка, мм;
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.