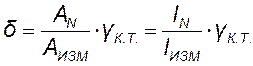Краткие сведения из теории и примеры решения задач. Предельное значение допускаемой абсолютной погрешности, страница 3

                            (12)

По формуле (12) вычисляем соответствующие относительные погрешности измерений двумя приборами, отличающиеся друг от друга только классом точност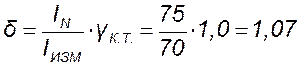и:

  и      .

Сравнивая эти два полученных значения относительной погрешности измерения (1,07 и 1,6) с заданным значением δ = 1,2 %, делаем вывод, что прибор из неравенства (11) с классом точности γ_КТ  =1,5 не обеспечивает заданной точности измерения, так как его ошибка измерения превышает заданную, а именно: 1,6 > 1,2. Что касается другого прибора из неравенства (11) с классом точности γ_КТ  =1,0 измерения, то этот прибор рациональным образом (наиболее дешевый) обеспечивает заданную точность измерения тока, так как его погрешность измерения δ = 1,07 % не превышает заданную δ = 1,2 %. Шкала амперметра имеет предел измерения 0 ─ 75 А.

Пример 2

Дано: - класс точности прибора γ_КТ  = 1,5;

- предельное значение шкалы амперметра (значение нормирующего множителя А_N ) I_N = 6,0 A;

- количество делений шкалы N = 30 делений;

- положение указателя (на каком делении установилась стрелка)  n= 24 деления.

Определить точность измерения (относительную погрешность δ) и записать результат этого однократного измерения в стандартной форме (1).

Решение

Вычислим цену деления и найдем измеренное значение тока

,

                          А_ИЗМ = I_ИЗМ = С·n = 0,2·24 = 4,8 А.

Найдем предельное допускаемое значение абсолютной погрешности

.

Оценим точность измерения

.

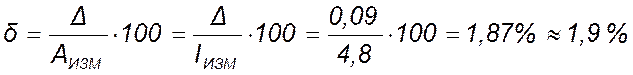Запишем ответ на задачу, учитывая правила записи округляемых чисел,I= (4,80 ± 0,09) A.

Пример 3

Дано: - характеристики амперметра (предельное значение I_N = 8A; класс точности γ_КТ  = 1,5; показания амперметра I_ИЗМ = 6 А);

- характеристики вольтметра (предельное значение U_N = 80 B; класс точности γ_КТ  = 0,5; показания вольтметра U_ИЗМ = 60 В);

- точность измерения δ = ± 4 %.

Записать результат в стандартной форме и оценить точность косвенного измерения мощности в сравнении с заданной.

Решение

Определим по результатам измерений тока и напряжения значение мощности

P = U·I = 60·6 = 360 Вт.

Вычислим по формуле (5) абсолютную погрешность косвенного измерения мощности, как полный дифференциал функции P = U·I  по переменным  U и I :

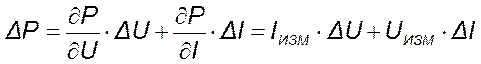,                (13)

где  ;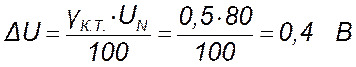

.

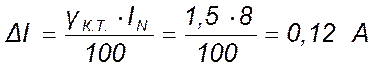С учетом полученных значений абсолютных погрешностей измерения напряжения ΔU и тока ΔI выражение (13) будет иметь вид:

ΔР = (6·0,4 + 60·0,12) Вт = 9,6 Вт.

Запишем результат косвенного измерения. Округление выполнить до двух значащих цифр.

Р = (360,0 ± 9,6) Вт.

Оценим точность косвенного измерения по формуле

.

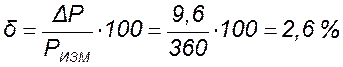Сравнивая полученную точность измерения δ = 2,6 % с заданным значением δ = 4 % , заключаем, что используемые средства косвенного измерения мощности, а именно: амперметр и вольтметр, обеспечивают заданную точность измерения.

Пример 4

Дано: Результаты многократных измерений U_i при i = 6

U₁ = 21,085 B;    U₂ = 21,093 B;   U₃ = 21,087 B;

U₄ = 21,084 B;   U₅ = 21,090 B;   U₆ = 21,082 B.

Найти значение измеренного напряжения и доверительный интервал с заданной доверительной вероятностью  Р = 0,99. Оценить точность измерения.

Решение

Определим наиболее вероятное значение измеряемой величины (математическое ожидание) по формуле

.

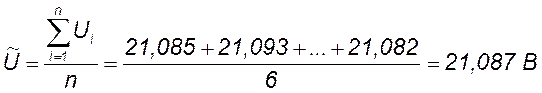Находим остаточные погрешности (случайные отклонения от среднего значения) с помощью математического выражения

.

 ρ₁ = - 2·10^-3 В;   ρ₂ = 6·10^-3 В;   ρ₃ = 0;   ρ₄ = - 3·10^-3 В; ρ₅ = 3·10^-3 В; ρ₆ = - 5·10^-3 В.

Проверим правильность вычисленных случайных отклонений по формуле

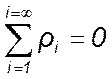.                                           (14)

В нашем примере .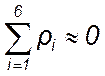

Найдем квадраты случайных отклонений и их сумму:

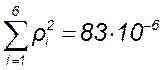 В².                                           

Определим среднеквадратичное отклонение (СКО) полученного ряда наблюдений по формуле

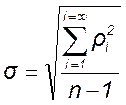=  = 4,07·10^-3 В.                     (15)

Выполним проверку на наличие промаха в результатах измерений. Для этого воспользуемся критерием Шовине. Из таблицы 3 приложения А «Справочные данные» определим коэффициент Шовине  К при n = 6. Этот коэффициент  К= 1,76.