Оценим наиболее вероятное среднеквадратичное отклонение многократных измерений тока
.
Из выражения (6) определим коэффициент распределения Стьюдента
.
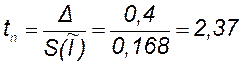Далее, с помощью таблицы 4 Приложения А «Справочные данные» считываем два соседних (ближайших от tn = 2,37 в большую и меньшую сторону) значений доверительной вероятности на строке n = 9. Такими соседними значениями доверительной вероятности будут Р1 = 0,95 при tn1 = 2,262 и Р2 = 0,96 при tn2 = 2,821, когда выполнено 9 измерений (n = 9).
Методом интерполяции вычисляем искомое значение доверительной вероятности с помощью формулы:
=
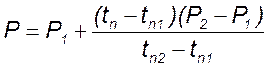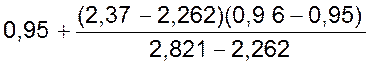= 0,95+0,002= =0,952.
Графическая иллюстрация нахождения доверительной вероятности методом интерполяции для рассматриваемого примера приведена на рис. 2.
 |
Запишем результат многократных измерений в требуемой стандартной форме с округлением до двух значащих цифр
I = (73,47 ± 0,40) при Р = 0,952.
Оценим точность произведенного измерения, то есть, определим относительную погрешность многократных измерений
.
Решение задачи выполнено полностью.
Иногда, при работе с табличными данными возникает необходимость использовать числовые величины, которые выходят за пределы значений таблицы. В этом случае необходимо воспользоваться методом экстраполяции и определить эти числовые данные, выходящие за пределы таблицы. Для этого строят график изменения табличных данных, используя хотя бы две соседние точки, одна из которых находится на границе таблицы. Далее продлевают график прямолинейным отрезком и считывают показания полученной третьей точки графика (уже вне таблицы), проекции которой удалены от края таблицы на расстояния, равные расстоянию между ранее упомянутыми соседними точками внутри таблицы.
2. Перечень задач расчетно-графической работы
Задача 1. Определите тип измерительного прибора (амперметр, вольтметр или ваттметр), а так же предельное оцифрованное значение шкалы и класс точности этого прибора для однократного измерения электрической величины с заданной относительной погрешностью δ. Исходные данные индивидуального задания указаны в таблице 5 приложения Б.
Задача 2. Определите точность однократного измерения (относительную погрешность δ) и запишите результат этого однократного измерения в стандартной форме. Исходные данные индивидуального задания указаны в таблице 6 приложения Б.
Задача 3. Запишите результат косвенного измерения мощности в стандартной форме и оцените его точность в сравнении с заданной относительной погрешностью δ = ± 5 %. Исходные данные индивидуального задания указаны в таблице 7 приложения Б.
Задача 4. Определите значение многократно измеренного напряжения и доверительный интервал этого измерения, если задана доверительная вероятность многократного измерения. Оцените точность измерения с учетом возможного промаха. Результат многократного измерения записать в стандартной форме. Исходные данные индивидуального задания указаны в таблице 8 приложения Б.
Задача 5. Запишите результат многократных измерений тока в стандартной форме и определите вероятность того, что истинное (средне статистическое, математическое ожидание) значение измеренного тока находится в пределах заданного доверительного интервала Δ. Исходные данные индивидуального задания указаны в таблице 9 приложения Б.
Приложение А
Справочные данные
Табл. 1. Предельные значения шкал измерительных приборов
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.