Краткие сведения из теории и примеры решения задач. Предельное значение допускаемой абсолютной погрешности, страница 4

По критерию Шовине промахом является i – ое измерение, если выполняется неравенство

                                              .                                      (16)

В нашем примере К·σ = 1,76·4,07·10^-3 = 7,16·10^-3 В и, следовательно, ни одно из значений случайных отклонений  ρ_i     по модулю не превышает величины 7,16·10^-3 В. Значит промахов нет.

Далее определим искомый доверительный интервал, используя распределение Стьюдента (6), представленное в виде числовых данных таблицы 4 приложения А «Справочные данные». Из таблицы 4 при n = 6 и Р = 0,99 считываем значение коэффициента Стьюдента  t_n = 3,707 и вычисляем значение доверительного интервала по формуле

,   где 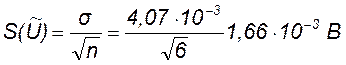   ─ наиболее вероятное значение средне квадратичного отклонения случайных замеров от их среднего значения.

                     Δ = 3,707·1,66·10^-3 = 0,006159 ≈ 0,006 В.

Запишем результат многократных измерений в стандартной форме

= (21,087 ± 0,006) B  при Р = 0,99.

Оценим точность многократных измерений, то есть определим относительную погрешность

.

Задача примера 4 решена.

Пример 5

Дано: - результаты многократного измерения тока I₁ = 73,28 A;  I₂ = 73,99 A;  I₃ = 70,98 A;  I₄ = 73,16 A;  I₅ = 73,04 A;  I₆ = 73,40 A;  I₇ = 73,63 A;  I₈ = 74,46 A;  I₉ = 73,45 A;  I₁₀ = 72,81 A.

- доверительный интервал   Δ = ± 0,4 А.

Записать результат многократных измерений в стандартной форме и определить вероятность того, что истинное (средне статистическое, математическое ожидание) значение измеренного тока находится в пределах заданного доверительного интервала Δ.

Решение

Определим наиболее вероятное (математическое ожидание, среднюю величину) значение тока

≈.

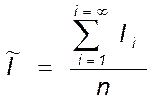Находим случайные отклонения (разброс) измерений по формуле

:

ρ₁ = 0,06 А; ρ₂ = 0,77 А; ρ₃ = - 2,24 А; ρ₄ = - 0,06 А; ρ₅ = -0,18 А; ρ₆ = 0,18А;  ρ₇ = 0,41 А;  ρ₈ = 1,24 А;  ρ₉ = 0,23 А;  ρ₁₀ = - 0,41 А.

Проверим правильность вычисления отклонений путем их алгебраического суммирования по формуле (14).

В нашем примере .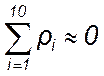

Находим квадраты случайных отклонений (разброса) и их сумму

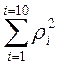= 36·10^-4+0,593+ … + 0,168 = 7,609 А².

Определяем среднеквадратичное отклонение многократных измерений с помощью выражения (15)

.

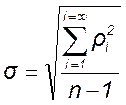
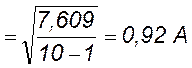Выполняем проверку на промах. Воспользуемся критерием Шовине и считываем значение коэффициента Шовине К = 2,06 из числовых данных таблицы 3 Приложения А «Справочные данные» при n = 10.

По критерию Шовине промахом является i – ое измерение, если выполняется неравенство

.

В нашем примере К·σ = 2,06·0,92 = 1,89 А и, значит, третье измерение (i = 3)является промахом, так как |-2,24| > 1,89. Это измерение необходимо исключить из ряда наблюдений и обработать результаты многократных измерений заново, но при n = 9.

Определим наиболее вероятное (математическое ожидание, среднюю величину) значение тока уже по результатам не 10-ти, а девяти измерений

≈.

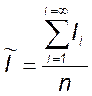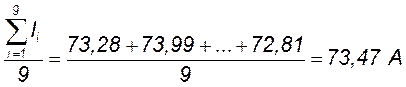Находим случайные отклонения (разброс) измерений по формуле

:

ρ₁ = - 0,19 А;  ρ₂ = 0,52 А;  ρ₃ = - 0,31 А;  ρ₄ = - 0,43 А;  ρ₅ = - 0,07А;  ρ₆ = 0,16А;   ρ₇ = 1,0 А;   ρ₈ = - 0,02 А;   ρ₉ = - 0,06 А.

Проверка правильности вычисления случайных отклонений заключается в подсчете их алгебраической суммы, которая должна быть близка к нулю. В нашем примере .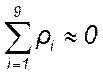

Находим квадраты случайных отклонений (разброса) и их сумму

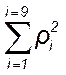= 0,0361+0,2704 + … + 36·10^-4 = 2,03 А².

Определяем среднеквадратичное отклонение многократных измерений                                           

.

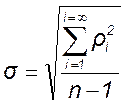
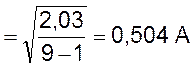Выполняем проверку на промах. Воспользуемся критерием Шовине и считываем среднее значение коэффициента Шовине К = 2,01 из числовых данных таблицы 3 Приложения А «Справочные данные» при n= 9, как среднее арифметическое при n= 8 и n= 10

.

По критерию Шовине промахом является i – ое измерение, если выполняется неравенство (16).

В нашем примере К·σ = 2,01·0,504 = 1,013 А и, следовательно, промахов нет, так как из девяти значений измеренного тока неравенство (16) не выполняется.