






Лекция 3 проф.
1. 5. Спектры непрерывных и решётчатых функций
На предыдущей лекции мы изучили взаимосвязи этих двух видов функций во временной области. Более того, мы сопоставили свойства дифференциальных и разностных уравнений, которые являются базой для получения математических моделей аналоговых и дискретных САУ. Теперь логично сопоставить их свойства в частотной области.
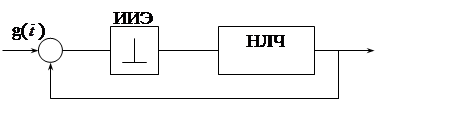
На рис. 1. 3 представлена функциональная схем некой дискретной (импульсной или цифровой) системы, где g(t) - непрерывный сигнал; ИИЭ – идеальный импульсный элемент с периодом квантования Т; НЛЧ - непрерывная линейная часть системы.
е(![]() ) e[n,
0]
) e[n,
0] ![]()
(-) Т
Рис. 1. 3.
Здесь непрерывный сигнал ошибки е (![]() ) квантуется ИИЭ и превращается в
решётчатую функцию e[n, 0], которая сглаживается, как фильтром, непрерывной
частью НЛЧ, формируя на выходе аналоговый сигнал
) квантуется ИИЭ и превращается в
решётчатую функцию e[n, 0], которая сглаживается, как фильтром, непрерывной
частью НЛЧ, формируя на выходе аналоговый сигнал ![]() .
Следовательно, в любой подобной ДСАУ имеются один и более ИИЭ, которые
преобразуют непрерывные функции времени в решётчатые. Изучим свойства
таких преобразований.
.
Следовательно, в любой подобной ДСАУ имеются один и более ИИЭ, которые
преобразуют непрерывные функции времени в решётчатые. Изучим свойства
таких преобразований.
В 1951г американский ученый Лайнвилл (Linwill W.K.[1])
предложил формулу преобразования Лапласа для РФ. Пусть ![]() – изображение по Лапласу
непрерывной огибающей функции, а
– изображение по Лапласу
непрерывной огибающей функции, а ![]() –
изображение по Лапласу соответствующей РФ. Тогда:
–
изображение по Лапласу соответствующей РФ. Тогда:
![]() ,
(1.3)1)
,
(1.3)1)
где
![]() - частота квантования.
- частота квантования.
Представим, что ![]() , и рассмотрим изображения
единичной функции и соответствующей ей РФ по Лапласу.
, и рассмотрим изображения
единичной функции и соответствующей ей РФ по Лапласу. ![]() - изображение единичного
сигнала. Его амплитудно-фазная характеристика
- изображение единичного
сигнала. Его амплитудно-фазная характеристика
_________________________________________________________________
1)Примечание 1. Есть небольшое, но практически важное
уточнение выражения (1. 3.). В работе [1] предлагается использовать его в таком
виде: ![]() +0,5 fT(0+),
в единственном случае. Если
+0,5 fT(0+),
в единственном случае. Если ![]() и
степень полинома A(s) только на единицу меньше
степени полинома B(s). Наше суждение о достоверности формулы (1. 3.)
приведено в конце текста лекции (примечание 4).
и
степень полинома A(s) только на единицу меньше
степени полинома B(s). Наше суждение о достоверности формулы (1. 3.)
приведено в конце текста лекции (примечание 4).
(АФХ)
будет: ![]() . Соответственно,
. Соответственно,
![]() ,
(2.3.)
,
(2.3.)
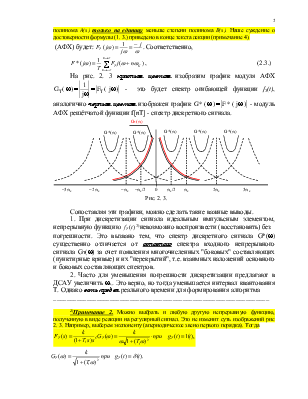
На рис. 2. 3 красным цветом изобразим
график модуля АФХ 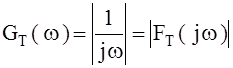 - это будет спектр
огибающей функции fT(t), аналогично черным цветом изображен
график
- это будет спектр
огибающей функции fT(t), аналогично черным цветом изображен
график ![]() - модуль АФХ решётчатой функции
f[nT] - спектр дискретного сигнала.
- модуль АФХ решётчатой функции
f[nT] - спектр дискретного сигнала.
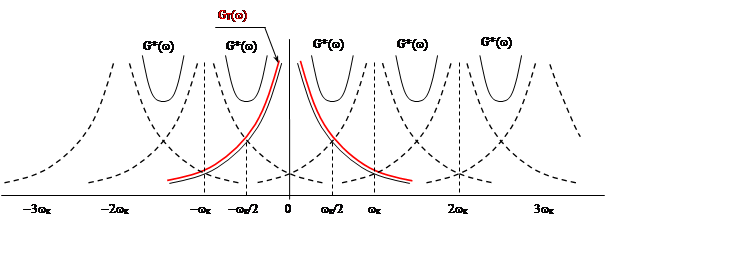
Рис. 2. 3.
Сопоставляя эти графики, можно сделать такие важные выводы.
1.
При дискретизации сигнала идеальным импульсным элементом, непрерывную функцию ![]() 2)невозможно
воспроизвести (восстановить) без погрешности.
Это вызвано тем, что спектр дискретного сигнала G*(w) существенно отличается от основного спектра
входного непрерывного сигнала GT(w) за счет появления
многочисленных "боковых" составляющих (пунктирные кривые) и их
"перекрытий", т.е. взаимных наложений основного и боковых
составляющих спектров.
2)невозможно
воспроизвести (восстановить) без погрешности.
Это вызвано тем, что спектр дискретного сигнала G*(w) существенно отличается от основного спектра
входного непрерывного сигнала GT(w) за счет появления
многочисленных "боковых" составляющих (пунктирные кривые) и их
"перекрытий", т.е. взаимных наложений основного и боковых
составляющих спектров.
2. Часто для уменьшения погрешности дискретизации предлагают в ДСАУ увеличить wк.. Это верно, но тогда уменьшается интервал квантования T. Однако есть предел реального времени для формирования алгоритма
_________________________________________________________________
2)Примечание 2. Можно выбрать и любую другую непрерывную функцию, полученную в виде реакции на регулярный сигнал. Это не изменит суть изображений рис 2. 3. Например, выберем экспоненту (апериодическое звено первого порядка). Тогда
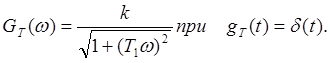
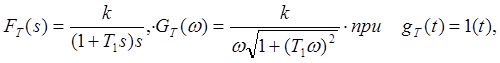
В первом случае записана реакция на
"единичный скачек", а во втором - на "дельта - импульс". Но
всегда ![]()
программной реализации
регулятора дискретной системы или другие физические ограничения.
Поэтому возможности уменьшения T ограничены пределом Tmin.
Если же известно, что в конкретной физическоймодели,
изучаемой (исследуемой или проектируемой) САУ, нет ограничений для выполнения
условия ![]() , то такую систему следует
изучать как непрерывную - аналоговую. Тогда свойства математической модели
такой САУ уже не будут иметь никакого отношения к данному курсу, что было
подчеркнуто во введении.
, то такую систему следует
изучать как непрерывную - аналоговую. Тогда свойства математической модели
такой САУ уже не будут иметь никакого отношения к данному курсу, что было
подчеркнуто во введении.
![]() 3.
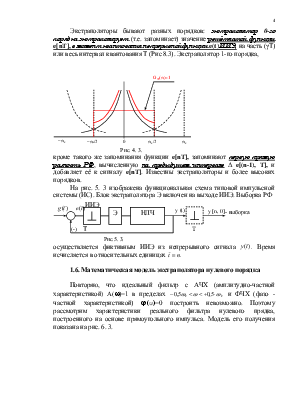
Многие авторы [1, 3, 6, 22 и др.] полагают возможным спектр огибающей
3.
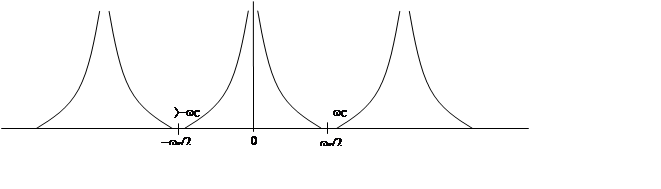
Многие авторы [1, 3, 6, 22 и др.] полагают возможным спектр огибающей ![]() ограничить частотой,
ограничить частотой, ![]() , при которой модуль спектра
, при которой модуль спектра ![]() равен нулю (см. рис 3. 3.). Тогда
остается (по их мнению) бороться только с "боковыми "составляющими
спектра РФ
равен нулю (см. рис 3. 3.). Тогда
остается (по их мнению) бороться только с "боковыми "составляющими
спектра РФ ![]() , но не с
"перекрытиями", которые максимальны при частотах
, но не с
"перекрытиями", которые максимальны при частотах ![]() .
.
![]()
![]()
![]()
![]()
ω1
ω3
Рис. 3. 3.
Такое предложение разумно для каких то систем, предназначенных только для отработки периодических воздействий с небольшим числом близких гармоник с частотами ω1 ω3 ω5 ω7 ω11 и убывающей амплитудой. Спектр такого сигнала представляет собою линии на указанных(±) частотах, (как на рис. 3. 3). Однако трудно представить практическое назначение электромеханической системы (ЭМС), отрабатывающей такие воздействия. При любых других регулярных сигналах (см. прим.1) избежать перекрытий в спектре РФ невозможно
Итак, изменение частоты квантования или даже ограничение модуля спектра входного непрерывного сигнала не освобождает дискретное преобразование информации от погрешности, связанной с наличием боковых составляющих спектра РФ в ДСАУ.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.