Спектры непрерывных и решётчатых функций. Свойства дифференциальных и разностных уравнений, страница 2

Таким образом, единственной возможностью уменьшить погрешность преобразования информации при дискретизации, является установка идеального фильтра с полосой пропускания  на выходе ИИЭ (рис. 4. 3). Поскольку идеальный фильтр физически невозможно построить, то применяют реальный фильтр - экстраполятор.

Экстраполяторы бывают разных порядков: экстраполятор 0-го порядка экстраполирует (т.е. запоминает) значение решётчатой функции e[nT], в момент квантования непрерывнойфункции e(t) ИИЭ, на часть (γΤ) или весь интервал квантования Т (Рис 8.3). Экстраполятор 1-го порядка,

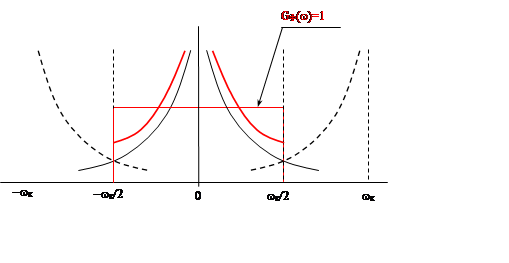
Рис. 4. 3.

кроме такого же запоминания функции e[nT], запоминают первую прямую разность РФ, вычисленную на предыдущем интервале Δ e[(n-1), T], и добавляет её к сигналу e[nT]. Известны экстраполяторы и более высоких порядков.

На рис. 5. 3 изображена функциональная схема типовой импульсной системы (ИС). Блок экстраполятора Э включен на выходе ИИЭ. Выборка РФ

Рис.5. 3.

осуществляется фиктивным ИИЭ из непрерывного сигнала . Время исчисляется в относительных единицах .

1.6. Математическая модель экстраполятора нулевого порядка

Повторяю, что идеальный фильтр с АЧХ (амплитудно-частной характеристикой) A(w)=1 в пределах  и ФЧХ (фазо - частной характеристикой) j (ω)=0 построить невозможно. Поэтому рассмотрим характеристики реального фильтра нулевого прядка, построенного на основе прямоугольного импульса. Модель его получения показана на рис. 6. 3.

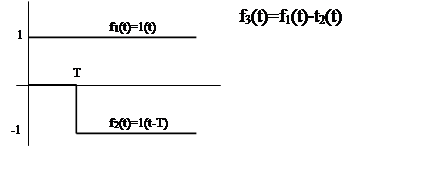
Рис. 6. 3.

Таким образом, экстраполированная функция на одном периоде определяется разностью двух единичных функций. Тогда вычислим и передаточную функцию такого экстраполятора по следующим формулам:

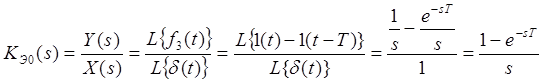,                   (3. 3)

c запоминанием на полный интервал квантования.

,                                                                                      (4. 3)

c запоминанием на часть  интервала квантования.

В этих формулах в качестве входного сигнала экстраполятора принята , которая формируется на выходе ИИЭ.

Получим частотные характеристики такого фильтра (4. 3.):

, тогда

 

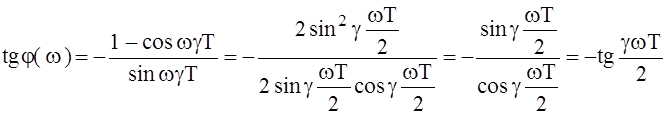
Итак, ФЧХ.

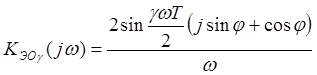; Модуль AЧХ  .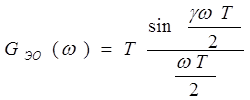

Рассмотрим те же характеристики при :

ФЧХ ; Модуль АЧХ 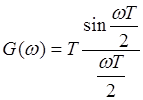.                                    (5. 3.)

Таблица 1

          Данные расчета АФХ экстраполятора нулевого порядка

w	0	wК/2	wК	1,5 wК	2 wК	2,5 wК	3 wК
G(w)	1	0,63	0	0,21	0	0,12	0
j(w)	0	-p/2	-p	-1,5p	-2p	-2,5p	-3p

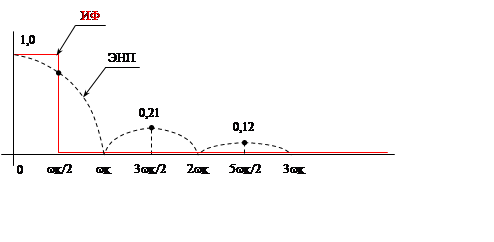
Рис. 7. 3.

Таким образом, получили, что характеристики реального фильтра - экстраполятора нулевого порядка отличаются от характеристик идеального фильтра. Но, в итоге, мы уменьшили погрешность преобразования информации в ДСАУ за счет существенного  подавления, как боковых составляющих спектра РФ, так и их перекрытий..

1.7. Функциональная схема  цифровой системы управления (ЦСУ)

До сих пор мы рассматривали функциональные схемы дискретных импульсных систем. Но какое отношение они имеют к современной реальной практике? Ведь известно, что подавляющее большинство современных ДСАУ построены как цифровые системы управления (ЦСУ). Попробуем разобраться в этом далеко непростом вопросе.

Рис. 8.3.

На рис.8.3 изображена функциональная схема реальной ЦСУ. Здесь принято: АЦП – аналого-цифровой преобразователь, ДР – дискретный регулятор, ЦАП – цифро - -аналовый преобразователь, НЧ – непрерывная часть САУ. Пока нас не интересует, как программно реализован ДР и на базе, каких  промышленных контроллеров или иных вычислительных устройств? Не раскрыт и состав блоков НЧ. Это вопросы последующих лекций. По существу же ЦСУ является нелинейной дискретной САУ. Её нелинейности создают преобразователи АЦП и ЦАП.

Математическая модель АЦП  представляет собой многопозиционного релейного устройства. Число позиций реле k (АЦП) и максимальное число выхода преобразователя N_макс (в десятичном коде) определяются формулой :N_макс=2^к-1.

 

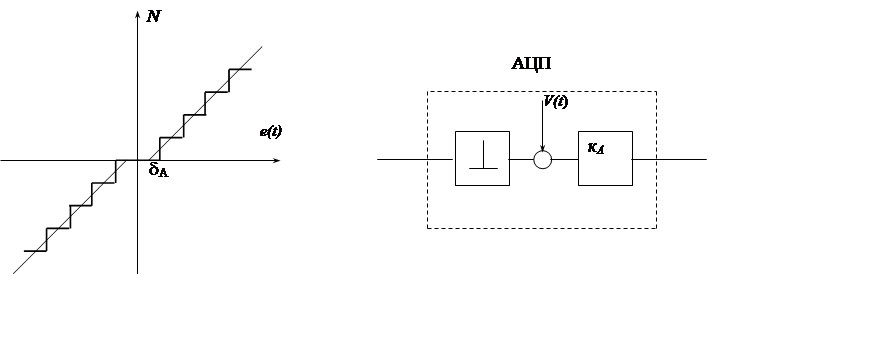
e(t)             e[nT]

Т

а)                                                                                     б)

Рис. 9. 3.

На рис. 9. 3, а изображена статическая характеристика АЦП. Её можно линеаризовать "секущей", если пренебречь уменьшением вдвое зоны нечувствительности при . Тогда коэффициент передачи преобразователя можно считать таким:. Динамическую  погрешность АЦП, вызванную отклонением его реальной "пилообразной " характеристики от  идеальной "секущей" v(t) можно считать случайным стационарным сигналом (помехой) с известными статистическими характеристиками[28].

На рис. 9. 3, б изображена динамическая модель  АЦП. Она представляет собой последовательное соединение ИИЭ и масштабирующего усилителя с коэффициентом передачи k_A. На вход ИИЭ подается сигнал e_x(t). На выходе ИИЭ сумма аналоговых сигналов e_x(t)+v(t), в моменты квантования³⁾, формируют число N_x, которое можно записать как РФ вида N_x [nT].