Спектры непрерывных и решётчатых функций. Свойства дифференциальных и разностных уравнений, страница 3

Статическая и динамическая части модели ЦАП представлены на рис. 10. 3, а и рис. 10.3, б.  При линеаризации характеристики секущей .

________________________________________________________________

³⁾Примечание3. Ошибочно полагать, что интервал квантования ИИЭ "Т" определяется частотой генератора тактовых импульсов (ГТИ), который входит в состав любого АЦП. Частоты квантования  современных ГТИ составляют сотни МГц и десятки ГГц. Поэтому эти дискретности моделей АЦП и ЦАП в математических  моделях ЦСУ и физических установках никогда не учитываются.Так чем же определяется длительность интервала квантования Т? Мы уже касались этого вопроса в выводе "2" на этой лекции.

Для будущих профессионалов стоит дать и более конкретное пояснение. Чаще всего это определяет практическое назначение ЦСУ. Поскольку Вам предстоит в ближайшем будущем  изучать курсы программного управления станками и роботами, то рассмотрим, в общих чертах, формирование алгоритма программного управления фрезерном металлорежущим станком. Рабочий инструмент - фреза приводится в движение (вращение) главным приводом , а в пространстве перемещается тремя отдельными следящими приводами подач (вверх - вниз, вправо - влево, вперед - назад). Обрабатываемое изделие закрепляют на "столе", который имееттакие же три отдельных следящих привода подач. Итак, необходимо реализовать одновременно взаимосвязанное управление до шести (или меньше) приводами. Работа такой взаимосвязанной САУ выполняется шагами - этапами.

Перечислим основные информационно - вычислительные действия на очередном этапе для перехода на следующий только для трех координатной системы привода фрезы.

Снятие и передача информации в УЧПУ (устройство числового программного управления) о реальном перемещении фрезы по каждой координате. Вычисление достигнутого положения фрезой в пространстве.

В УЧПУ следует выполнить сравнение достигнутых и задаваемых положений фрезы на предыдущем шаге и вычислить поправки параметров движения инструмента для последующего шага. Вычислить перемещения и скорости всех трех координатных приводов на последующем шаге с учетом поправок.

Должна быть проверена возможность таких движений приводами подач для обеспечения заданного качества выполнения технологической операции.

Введены необходимые поправки в программы дискретных регуляторов координатных приводов. Введены вычисленные задания управления одновременно на АЦП всех координатных приводов.

Подсчет времени выполнения всех элементарных операций этого алгоритма и определяет длительность интервала квантования Т. При этом скорости движений следящих приводов в рабочем режиме на таких станках составляют 10 м./мин и более

Итак, главный вывод: типового ответа на этот вопрос нет. Ответ определяется свойствами рабочего (технологического) процесса и комплексом требований к ЭМС и  технологическому оборудованию.

На вход  динамической  части модели ЦАП, кроме цифрового сигнала управления N, поступает случайная стационарная помеха v_ц (t), а на выходе включен экстраполятор нулевого порядка (ЭНП).

Т

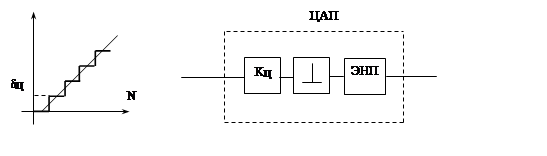
v_ц (t)

N

а)                         Рис. 10. 3.         б).

При сформулированных выше условиях линеаризации характеристик АЦП и ЦАП нелинейную модель ЦСУ (см. рис. 8. 3) можно заменить линеаризованной моделью ЦСУ, изображенной на рис. 11. 3.

        Т                                               Т

Рис. 11. 3.

Если взять преобразователи с одинаковыми квантами: , то и схема 11. 3. может быть упрощена. Полученная структура изображена на рис. 12. 3.

T                                                       T

g(t)     e(t)                                                                                                              y(t)

Рис. 12. 3.

В итоге мы получили импульсную систему управления. Итак, математическая модель линеаризованной цифровой системы является типовой импульсной системой.

Примечание 4.  Приведем полученное нами нестрогое доказательство справедливости выражения (1. 3).

Для записи РФ используем формулу (4. 1): f [nT]=f_T(t)δ(t - nT). Для представления  используем обратное преобразование Фурье 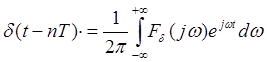,   (6. 3)

где  спектр

Учитывая дискретность  сигнала , можно в правой части (6. 3) интеграл заменить суммой 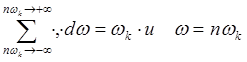. После этих подстановок в (6. 3) перепишем это выражение в таком виде:

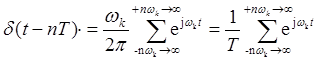                                                                     (6.3.)¹

Изображение по Лапласу решетчатой функции будет получено в таком виде:

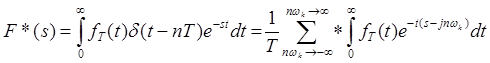.                                     (7. 3)

Интеграл в выражении (7. 3), есть изображение непрерывной огибающей функции, но со сдвигом в области аргумента на величину , т.е. .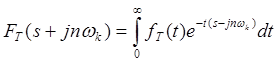

Таким образом, получено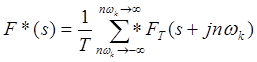,                                         (8. 3)

что равносильно выражению (1. 3).(С. К.).

Скорректировано 18.02.09.