противном случае, если ![]() , делается противоположный вывод, и
для аппроксимации применяется ОМНК (пп. 2.3.7.2, 2.3.7.6).
, делается противоположный вывод, и
для аппроксимации применяется ОМНК (пп. 2.3.7.2, 2.3.7.6).
2.5.6.2. Проверка гипотезы о степени аппроксимирующего полинома,
характеристики погрешностей измерений известны.
a) Измерения однократные.
Постановка задачи
полиномиальной аппроксимации некоторой исследуемой функции y = f(x) и
метод ее решения изложены в в пп. 2.3.7.1, 2.3.7.2. В соответствии с
материалами этих пунктов исходными данными для полиномиальной аппроксимации
функции y = f(x) являются ее значения в k дискретных точках,
возмущенные погрешностями. Эти значения были объединены в вектор ![]() . С другой стороны, вектор точных
значений аппроксимируемой функции выражался, как
. С другой стороны, вектор точных
значений аппроксимируемой функции выражался, как ![]() , где
, где ![]() - вектор точных значений коэффициентов искомого полинома.
Степень искомого полинома q полагалась известной, а погрешности -
распределенными нормально:
- вектор точных значений коэффициентов искомого полинома.
Степень искомого полинома q полагалась известной, а погрешности -
распределенными нормально: ![]() . Тогда вектор отсчетов также распределен нормально:
. Тогда вектор отсчетов также распределен нормально: ![]() , то есть
, то есть ![]() . Эта ситуация именовалась, как
случай известной модели.
. Эта ситуация именовалась, как
случай известной модели.
В п. 2.3.7.2 были
получены ММП - оценки ![]() коэффициентов путем минимизации квадратичных форм
коэффициентов путем минимизации квадратичных форм
- ![]() - в случае равноточных измерений и
применения МНК,
- в случае равноточных измерений и
применения МНК,
- ![]() - в случае неравноточных измерений и
применения ОМНК.
- в случае неравноточных измерений и
применения ОМНК.
Из-за случайности
погрешностей измерений оценки ![]() также случайны, а значит, случайными являются векторы
также случайны, а значит, случайными являются векторы ![]() и вслед за ними - квадратичные
формы, которые определены в п. 2.3.7.2:
и вслед за ними - квадратичные
формы, которые определены в п. 2.3.7.2:
- ![]() - в случае применения МНК
- в случае применения МНК
- ![]() - в случае применения ОМНК.
- в случае применения ОМНК.
Поскольку найденные оценки коэффициентов несмещены,
![]() .
.
В п. 2.3.7.3 приведены плотности распределения этих квадратичных форм в условиях, когда плотности распределения погрешностей нормальны и модель известна. Плотности распределения обеих квадратичных форм одинаковы: это плотность распределения “хи - квадрат” с (k - q - 1) степенями свободы, то есть
![]() .
.
На практике модель
практически никогда не бывает известной. Тогда, при ошибочном назначении
степени p аппроксимирующего полинома, меньшей, чем истинная степень q,
оценки коэффициентов оказываются смещенными (см. также п. 2.3.7.4, замечание
4), поэтому ![]() , значения
, значения ![]() существенно возрастают, и плотность
распределения изменяется. При увеличении степени аппроксимирующего полинома и,
в особенности, при p > q ухудшается обусловленность матриц
существенно возрастают, и плотность
распределения изменяется. При увеличении степени аппроксимирующего полинома и,
в особенности, при p > q ухудшается обусловленность матриц ![]() и
и ![]() , и теряется вычислительная устойчивость МНК и ОМНК (см. п.
2.3.7.7). Поэтому случаи, когда p > q , не рассматриваются.
, и теряется вычислительная устойчивость МНК и ОМНК (см. п.
2.3.7.7). Поэтому случаи, когда p > q , не рассматриваются.
Итак, пусть в изложенных
условиях при истинной степени аппроксимирующего полинома q была
назначена степень p < q,
и с помощью МНК или ОМНК получены оценки p + 1 коэффициента. Обозначим
вектор найденных таким образом оценок через ![]() , а квадратичные формы, вычисленные при этих значениях оценок
- через
, а квадратичные формы, вычисленные при этих значениях оценок
- через ![]() .
.
Сформулируем гипотезу.
![]() степень аппроксимирующего
полинома p = q,
степень аппроксимирующего
полинома p = q,
![]() степень аппроксимирующего
полинома p < q.
степень аппроксимирующего
полинома p < q.
Статистикой критерия
проверки этой гипотезы является величина ![]() , которая при p = q, то есть при справедливости
нулевой гипотезы равна
, которая при p = q, то есть при справедливости
нулевой гипотезы равна ![]() и распределена, как
и распределена, как ![]() (см. п. 2.3.7.3). Поэтому в качестве критического значения
при заданной вероятности a выбирается (1 - a)×100 - процентная квантиль из таблицы квантилей распределения “хи -
квадрат” с (k - q - 1) степенями свободы.
(см. п. 2.3.7.3). Поэтому в качестве критического значения
при заданной вероятности a выбирается (1 - a)×100 - процентная квантиль из таблицы квантилей распределения “хи -
квадрат” с (k - q - 1) степенями свободы.
Процедура проверки гипотезы в условиях, когда заданы вид полинома (степенной, обобщенный по п. 2.3.7.9) и вероятность a.
1. Оцениваются коэффициенты полинома
![]() или
или ![]() .
.
2. Вычисляется статистика критерия
![]() или
или ![]() .
.
3. Значение статистики ![]() сравнивается с критическим
значением:
сравнивается с критическим
значением:
- если ![]() , делается вывод о том, что нет
достаточных оснований для того, чтобы отвергнуть нулевую гипотезу,
, делается вывод о том, что нет
достаточных оснований для того, чтобы отвергнуть нулевую гипотезу,
- в противном случае,
если ![]() , делается вывод о том, что нет
достаточных оснований для того, чтобы считать нулевую гипотезу справедливой.
, делается вывод о том, что нет
достаточных оснований для того, чтобы считать нулевую гипотезу справедливой.
b) Измерения многократные.
Этот случай отличается от
предыдущего тем, что в качестве исходных данных для полиномиальной
аппроксимации используется не вектор результатов однократных измерений ![]() , а вектор средних арифметических
значений
, а вектор средних арифметических
значений ![]() результатов многократных измерений.
В условиях, перечисленных выше в п. a), вектор средних
арифметических обладает свойствами (см. также пп. 2.3.4.3, 2.3.7.5) :
результатов многократных измерений.
В условиях, перечисленных выше в п. a), вектор средних
арифметических обладает свойствами (см. также пп. 2.3.4.3, 2.3.7.5) :
![]() ,
, 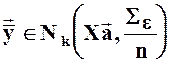 ,
, ![]() .
.
В случае равноточных измерений, когда применяется МНК,
![]()
![]() , где E - единичная матрица (см.
также п. 2.3.7.2) .
, где E - единичная матрица (см.
также п. 2.3.7.2) .
Тогда, если для
аппроксимации назначена степень полинома p, и ![]() - вектор оценок (p + 1) коэффициента этого полинома, то
статистикой критерия проверки гипотезы о степени полинома будет
- вектор оценок (p + 1) коэффициента этого полинома, то
статистикой критерия проверки гипотезы о степени полинома будет
![]() .
.
В случае, когда измерения равноточные и применяется МНК,
![]() .
.
Как и ранее, при условии
справедливости нулевой гипотезы, то есть при p = q ![]() и
и ![]() . Критическое значение при заданном
значении вероятности a
есть
. Критическое значение при заданном
значении вероятности a
есть ![]() .
.
Гипотеза формулируется по аналогии с формулировкой, приведенной в предыдущем п. a).
![]() степень аппроксимирующего
полинома p = q,
степень аппроксимирующего
полинома p = q,
![]() степень аппроксимирующего
полинома p < q.
степень аппроксимирующего
полинома p < q.
Процедура проверки гипотезы в условиях, когда заданы вид полинома (степенной, обобщенный по п. 2.3.7.9) и вероятность a.
1. Оцениваются коэффициенты полинома
![]() или
или ![]() .
.
2. Вычисляется статистика критерия
![]() или
или ![]() .
.
3. Значение статистики ![]() сравнивается с критическим
значением:
сравнивается с критическим
значением:
- если ![]() , делается вывод о том, что нет
достаточных оснований для того, чтобы отвергнуть нулевую гипотезу,
, делается вывод о том, что нет
достаточных оснований для того, чтобы отвергнуть нулевую гипотезу,
- в противном случае,
если ![]() , делается вывод о том, что нет
достаточных
, делается вывод о том, что нет
достаточных
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.