Задача синтеза систем автоматического управления. Основные понятия и определения. Требования к электромеханической системе, страница 8

Приведенная классификация методов является условной, и при этом далеко не исчерпывающей. Рассмотрим некоторые из перечисленных методов более подробно.

Синтез по преобладающим (детерминирующим) корням. 1948г. Т.Н.Соколов.  Автор исходит из того, что переходный процесс в сколь угодно сложной линейной системе определяется только детерминирующими корнями характеристического уравнения замкнутой системы. Характеристическое уравнение системы при наличии пары детерминированных корней можно представить в виде:

, где коэффициенты b₁ и b₂   << c_i.

А для случая трех детерминирующих корней:

, при b₁ , b₂ и b₃   << c_i.

Детерминирующие корни, с одной стороны, определяют характер переходного процесса, а с другой - коэффициенты характеристического уравнения. Остается подобрать параметры корректирующего устройства, чтоб характеристическое уравнение приобрело желаемый вид. Данный метод удобен, когда при известной структуре и заданном коэффициенте усиления необходимо подобрать величину какой-либо одной постоянной времени. Ограничения: в сложных системах необходимые значения коэффициентов характеристического уравнения не всегда могут получены выбором корректирующего устройства.

Метод корневых годографов. На плоскости корней наносится кривая изменения корней характеристического уравнения в зависимости от какого-либо параметра системы (при постоянных остальных параметрах). Затем выбирается такое значение этого параметра, при котором корни уравнения наиболее благоприятны с точки зрения опять же качества переходной характеристики. Понятно, что если известны нули и полюса передаточной функции системы, то определить показатели переходной характеристики не составляет труда. По крайней мере можно воспользоваться детерминирующими корнями: . Приближенные значения показателей качества системы определяются формулами:  ,  …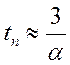

В литературе и справочниках можно найти графики зависимостей s(x),  М(s). Разработаны таблицы, в которых по нулям и полюсам системы можно найти точные коэффициенты переходной характеристики. Результаты будут значительно точнее, если в рассмотрение берутся три детерминирующих корня (один вещественный и пара комплексных).

Метод стандартных передаточных функций. А.А. Красовский. Предполагается выбор параметров элементов САУ с заданной структурой, при которой коэффициенты ее передаточной функции принимают заранее заданные (стандартные) значения, обеспечивающие удовлетворение требований к динамическим свойствам системы. При этом и переходная характеристика системы будет иметь заранее известную форму. Метод основан на использовании специальных таблиц со стандартными коэффициентами, определяющими переходную характеристику. Для определения параметров САУ (параметров корректирующего устройства) составляется система уравнений. После ее решения выбираются эти параметры. Применение данного метода ограничено. Недостатком является то, что одновременно выбираются все коэффициенты передаточной функции и необходимо иметь n варьируемых параметров. Необходимые параметры не всегда могут быть реализованы прежде всего из-за малого перерегулирования стандартных (табличных) переходных характеристик.

Типовые характеристические уравнения. В.Н. Яворский. Даются стандартные наборы коэффициентов характеристического уравнения разных степеней (в таблице). Для каждого уравнения указаны показатели качества соответствующей ему переходной характеристики. Для получения параметров корректирующего устройства также необходимо составить систему уравнений и решить ее. Типовые характеристические уравнения дают широкую возможность удовлетворения требований к динамическим свойствам САУ. Предложены типовые уравнения до 12 порядка включительно.