Задача синтеза систем автоматического управления. Основные понятия и определения. Требования к электромеханической системе, страница 10

Использование стандартных ЛАХ. Существует класс систем, у которых в разомкнутом состоянии ПФ имеет вид:             

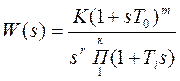, где

r-  степень астатизма,

m-  порядок полинома в числителе ПФ

k-  порядок полинома в знаменателе ПФ (с учетом r).

Коэффициенты ошибок высчитаны заранее по  s_м и t_п.

Стандартно среднечастотная зона ЛАХ проходит под наклоном -1.

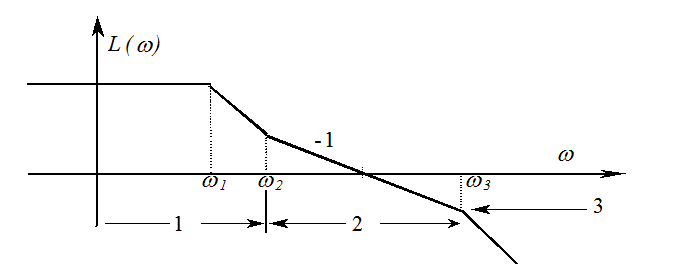
1 - низкочастотная, 2 - среднечастотная, 3 - высокочастотная области ЛАХ.

Низкочастотная область определяет качество установившихся процессов, то есть определяет точность отработки входных воздействий.

Форма ЛАХ в 1 зоне определяется исходя из заданной точности с учетом вида входного воздействия и выражений для коэффициентов ошибок.

Остальную часть ЛАХ выбирают исходя из следующих соображений:

1.  Наклон  -1 (среднечастотная область).

2.  Высокочастотная область (зона 3) выбирается из условия максимальной простоты коррекции, так как высокочастотная зона определяет быстрозатухающие экспоненты переходного процесса и проявляется только на начальной части переходного процесса.

Недостаток - очень трудно учесть влияние возмущений и нестабильность параметров системы.

Такой синтез не обладает свойствами оптимальности.

Использование ПФ с типовыми переходными процессами. Для некоторого ряда значений s_м и t_п получены ПФ, соответствующие системам с такими характеристиками.

Располагая ПФ нескорректированной системы, подбирают ближайшую (похожую) желаемую ПФ с требуемыми показателями точности и качества переходного процесса: . Далее строится ЛАХ .  Остальное - просто.

Достоинства метода: Простота и малый объем вычислений.

Недостатки: Нет возможности учесть возмущения и нестабильность параметров. Методика применима только для астатических систем 1 и 2 порядков.

Но идея - очень замечательная!

Динамический синтез с использованием запретных зон. В отличие от рассмотренных способов построения  данный метод является оптимальный. Повышение точности отработки входного воздействия заставляет увеличивать коэффициент усиления. Улучшение переходного процесса за счет повышения запаса устойчивости заставляет увеличивать w_ср.  И та и другая причины приводят к расширению полосы пропускания системы. Бесекерский ввел функционал, минимизация которого сужает полосу пропускания. В столкновении этих тенденций определяется оптимальное решение.

Методы синтеза по минимуму интегральной оценки качества. Данные методы используются для определения параметров корректирующих устройств при заданной структуре САУ. Задача синтеза формулируется таким образом, что при заданной структуре системы, одни параметры которой заданы, а другие можно изменять, требуется отыскать такие значения изменяемых параметров, при которых некоторая интегральная оценка качества становится минимальной. Чаще всего используются квадратичная или улучшенная квадратичная интегральная оценки. Сформулированная задача является задачей параметрической оптимизации и относится к классу экстремальных задач. Можно пытаться решать ее аналитически, но при относительно больших порядках реальных систем целесообразно воспользоваться численными методами решения экстремальных задач, методами, позволяющими отыскать набор варьируемых параметров системы, доставляющих минимум (экстремум) заданному функционалу качества при известных ограничениях. Для этой цели разработано множество методов поиска минимума функционала по N и по одной переменным. К таковым относятся ряд градиентных методов, методы золотого сечения, парабол и другие. Несмотря на кажущуюся сложность сформулированной задачи, она легко формализуется, и при использовании вычислительной техники значительно быстро удается получить искомый результат. При синтезе удается учесть многие нелинейности и ограничения, присущие реальной систем.