Задача синтеза систем автоматического управления. Основные понятия и определения. Требования к электромеханической системе, страница 5

Полученные соотношения объясняют необходимость повышения точности и стабильности задающих устройств, датчиков обратной связи и прочих элементов системы с целью обеспечения заданной точности.

Кроме названных требуемая точность системы может быть достигнута применением других приемов.

Коррекция входного сигнала

Добиться увеличения астатизма системы можно соответствующим выбором безынерционного преобразовательного элемента на входе системы:

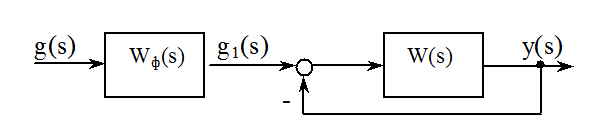
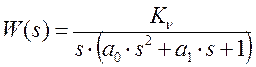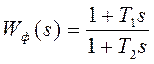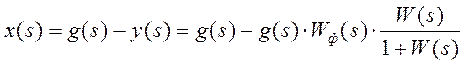Пусть объект имеет передаточную функцию , а передаточная функция фильтра , причем .  Ошибка в системе . После подстановки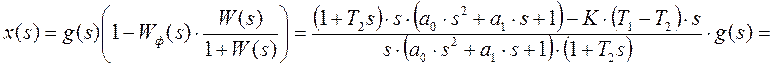

.   

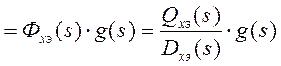Если параметры фильтра подобрать таким образом, чтоб выполнялось соотношение , то в числителе передаточной функции системы по ошибке  будут отсутствовать члены с s  в степени 1 и 0.

Получили астатизм второго порядка (ничего кардинального не предпринимая!!!). Благодаря введению входного фильтра с определенными параметрами удалось достичь качества отработки входного воздействия как в системе с астатизмом второго порядка при исходной системе с астатизмом первого порядка. В то же время никакого ухудшения устойчивости системы не произошло, так как замкнутая часть системы с астатизмом первого порядка структурно устойчива. Впрочем, при отклонении передаточного коэффициента разомкнутой системы от расчетного значения появляется установившаяся ошибка, пропорциональная величине отклонения. Данный метод имеет несомненные преимущества из-за своей простоты. Астатизма можно добиться и в случае системы со статическим замкнутым контуром. Однако применение такого подхода возможно только при отсутствии помех в задающем сигнале и стабильных параметрах системы.

Введение неединичных обратных связей

Неединичная обратная связь позволяет также обеспечить астатизм (или повысить его порядок) относительно задающего воздействия.

Так, в системе с единичной обратной связью

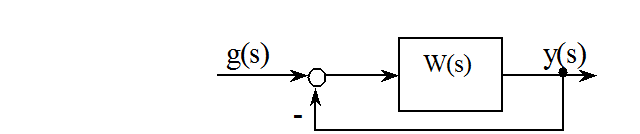
при  (случай статической системы) 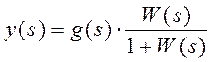,       ,  принципиально должна быть ошибка:    .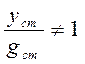

Введем в систему обратную связь:  ,    .

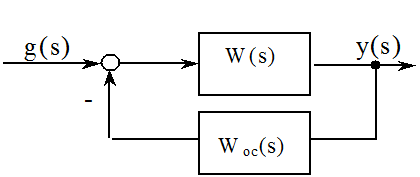
Тогда ,    ,     .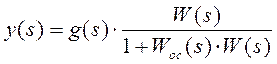

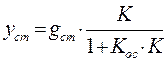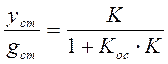Можно потребовать, чтобы выполнялось равенство  ,   то есть  ,    откуда для того, чтобы система отрабатывала входное воздействие без статической ошибки, необходимо ввести в систему такую обратную связь, статический коэффициент передачи которой   . Но неточность расчета и нестабильность параметров системы (передаточного коэффициента разомкнутой системы) служат причиной появления статической ошибки слежения.

Использование инвариантности по возмущению

Возмущения являются одними из причин появления ошибок в системе: 

X_f(s)=Ф_xf(s)×f(s).

Инвариантность - независимость выходного сигнала от возмущения. Инвариантность бывает абсолютная и частичная. Абсолютная инвариантность: X_f(s) = 0;  частичная:  | X_f(s)| < e.   Любой вид инвариантности связан с какой-то компенсацией действия возмущения.

Существует четыре формы инвариантности.

1. Если f(s) = 0  и  Ф_xf(s) ¹ 0, то X_f(s) = 0.

2. Если f(s) ¹ 0  и  Ф_xf(s) = 0    и а) имеется лишь один канал воздействия возмущения, то X_f(s) = 0.

б) есть несколько путей для возмущения и

, но  , то также  X_f(s) = 0.

3. Если f(s) ¹ 0  и  Ф_xf(s) ¹ 0 , но Ф_xf(s)×f(s)=0.

Например, если возмущение представляет собой постоянную величину, а ошибка из-за него нежелательна и, если можно обеспечить, чтобы в числителе Ф_xf(s)        был множитель s, то это постоянное возмущение не даст своей составляющей в ошибке, так как производная возмущения равна нулю.

4. Для достижения инвариантности системы к возмущениям применяются средства специальной компенсации возмущения (компаундирующие связи). При компаундирующей связи, образующей второй канал воздействия возмущения, несмотря на большие возможности по достижению инвариантности, имеет место отрицательное влияние на устойчивости системы, так как в некоторых случаях образуется положительная обратная связь. Правда, это влияние может быть скомпенсировано специальным корректирующим устройством в прямой цепи системы. Компаундирующая связь, не образующая второго канала возмущения, весьма значительно влияет на устойчивость и качество воспроизведения задающего воздействия, поэтому корректирующее устройство в прямой цепи необходимо.