Системы подчиненного управления. Основы теории. Системы с параллельной и смешанной коррекцией, страница 6

Коэффициент при S в знаменателе передаточной функции регулятора представляет собой постоянную интегрирования и в простейшем случае равен . При выводе этой зависимости ранее предполагалось, что все малые постоянные времени представляют собой малые инерционности, сосредоточенные в прямом канале. Между тем, на практике малые постоянные встречаются как в прямом канале, так и в канале обратной связи.

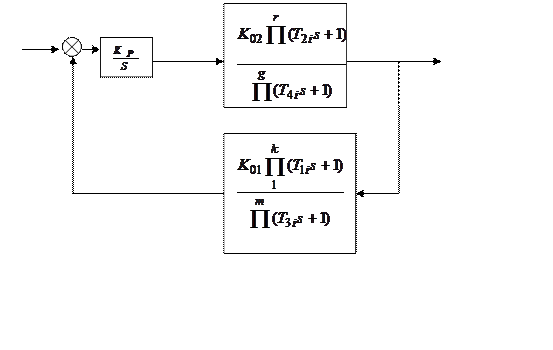
Рис. 9

Для определения величины В₀ при наиболее общей структуре контура регулирования служит формула Д.С.Ямпольского (Ямпольский С.Д.  Электричество, №6, 1969, стр.24-29)

:

.

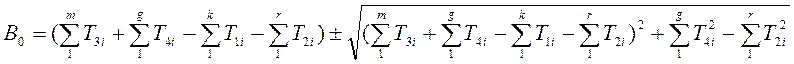Физический смысл  имеет только  Рассмотрим несколько распространенных на практике случаев.

1.  Малые постоянные есть только в прямом канале регулирования, малые упреждения отсутствуют, т.е. ;  тогда .

2.  Малые инерционности есть как в прямом канале, так и в канале обратной связи; малые упреждения отсутствуют, т.е. ; , тогда

.

Эта формула важна, т.к. рассмотренный случай является наиболее распространенным на практике, что обусловлено инерционностью большинства применяемых датчиков  и необходимостью установки фильтров в цепи обратной связи (например, для фильтрации напряжения тахогенератора).

3.   Малые инерционности имеются только в прямом канале, малые упреждения имеются только в канале обратной связи, т.е.  В этом случае                                   

.

При подкоренное выражение отрицательно, что лишает В₀ физического смысла. Это означает, что при таком соотношении параметров оптимизируемого контура модульный оптимум не достигается. Следует отметить, что в этом случае существует возможность повышения быстродействия контура за счет  увеличения коэффициента регулятора без появления перерегулирования.

В тех случаях, когда требуется повысить усиление регулятора по сравнению с усилением, соответствующем настройке по модульному оптимуму, целесообразно вводить в канал обратной связи форсирующие звенья, создающие необходимое упреждение. Однако, при этом необходимо учитывать возможность снижения помехоустойчивости системы.

Если в третьем случае соотношение параметров таково, что , то существуют два значения В₀, из которых для расчета настройки регулятора следует выбирать большее. Полученное таким образом значение В₀ используется для определения оптимальных параметров регулятора.

                    Передаточная функция замкнутого оптимизированного контура определяется формулой

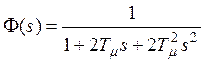,  где .

При рассмотрении наиболее общей структуры контура регулирования не учитывалась возможность нахождения в составе объекта малого колебательного звена с передаточной функцией вида  , некомпенсированного действием регулятора. Такой случай наблюдается при настройке контура, в состав которого входит замкнутый подчиненный контур. В большинстве случаев "малое колебательное звено" можно с достаточной точностью можно заменить инерционным звеном с передаточной функцией . 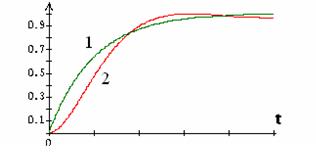Такое предположение основывается на "близости" переходных характеристик указанных звеньев

Рис.10    Переходные характеристики инерционного звена -1 и звена второго порядка –2.

При отсутствии в составе объекта других звеньев с малыми постоянными времени замена звена второго порядка инерционным звеном приводит к отклонению переходного процесса оптимизируемого контура  от стандартного:

при   настройка контура очень мало отличается от оптимальной настройки. При   заметно возрастает перерегулирование. Для  , т.е.  при  наличии в составе объекта замкнутого оптимизированного  по модульному оптимуму контура, перерегулирование составляет 8%. Если такая величина приемлема, то можно принять . При наличии других малых постоянных времени величина перерегулирования   будет находиться в пределах 4-8%, что приемлемо для большинства практических случаев. Если же требуется стандартная величина перерегулирования 4,3%, то при величину T_3i  принимают равной  .