Информатика и выч. техника \ Системное программное обеспечение

Системы подчиненного управления. Основы теории. Системы с параллельной и смешанной коррекцией, страница 2

Время до момента, когда регулируемая величина первый раз пересечет уровень нового установившегося значения называется временем первого согласования;

Время , до окончательного попадания регулируемой величины в зону нового установившегося значения шириной , является временем переходного процесса;

Амплитуда перерегулирования .

Передаточная функция контура регулирования не может быть равна её желаемому значению Это неравенство относится ко всему спектру частот, от нулевой до бесконечно большой. Очевидно, целесообразно добиться по крайней мере для части спектра частот, точнее для полосы частот от нуля до возможно большей величины, такого положения, чтобы модуль передаточной функции в этой полосе стремился к единице

Так как модуль передаточной функции в течение всего переходного процесса должен быть возможно ближе, т.е. прилегать, к единице, то такой прием называют оптимизацией настройки регулятора путём "пригонки" модуля к единице. При использовании такого приёма обеспечивается устойчивость контура регулирования, поэтому исследовать контур на устойчивость становится не нужным.

Пригонка модуля к единице характеризуется тем, что должна оставаться близкой к "1" даже при Таким образом, кривая зависимости имеет горизонтальную касательную при нулевой частоте. Эта горизонтальность должна сохраняться до возможно более высоких частот.

При анализе контуров регулирования постоянно будем иметь дело с передаточными функциями двух характерных типов

и .

Так как эти передаточные функции получаются из анализа разомкнутых контуров, то и В некоторых случаях b1 может быть равна нулю.

Если записать уравнение для модуля передаточной функции

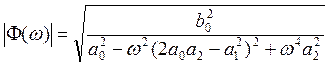и потребовать, чтобы выражение оставалось равным единице при низких частотах (вплоть до нулевой), то получим . Это первое условие оптимизации.

Применяя аналогичные приёмы к уравнению второго типа, найдем

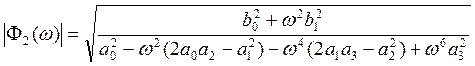Для пригонки этого модуля к единице надо потребовать выполнения следующих условий: ; Если эти условия выполняются, то уравнения приобретают вид:

, .

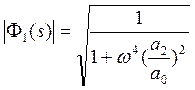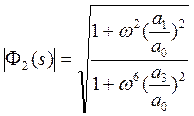Из изложенного следует, что добиться точного равенства единице модуля передаточной функции можно только при нулевой частоте. Однако, при весьма низких частотах вполне достижимо хорошее приближение к единице.

Сумма малых постоянных времени

Предположим, что объект управления содержит большое количество инерционных звеньев, причем сумма постоянных времени этих звеньев равна :

Передаточная функция разомкнутого контура, который кроме указанных звеньев содержит еще и интегрирующее звено, имеет вид:

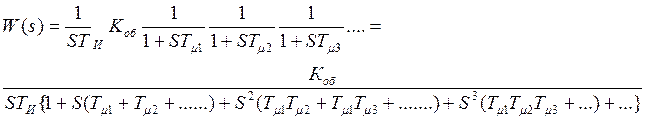Сравнивая реакцию разомкнутого контура, содержащего инерционное звено с постоянной времени , на скачек управляющего воздействия с такой же реакцией контура, содержащего многие постоянные времени, можно заметить , что кривые похожи друг на друга.

y y