Системы подчиненного управления. Основы теории. Системы с параллельной и смешанной коррекцией, страница 4

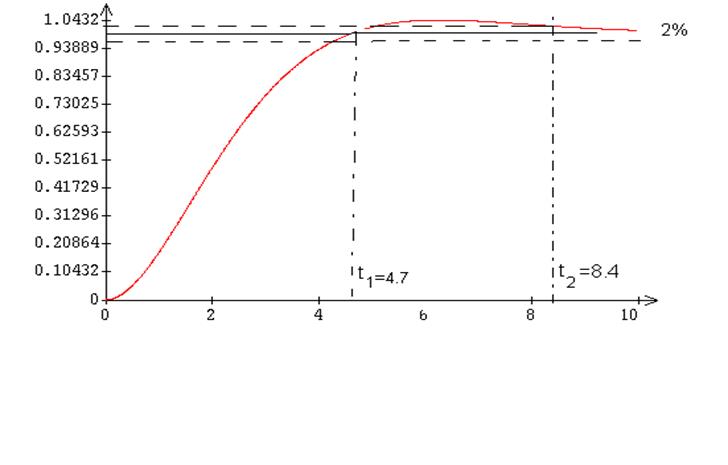
Уравнения и переходная функция, показанная на рисунке, являются типичными для любого контура, оптимизированного по модулю передаточной функции, независимо от конкретного исполнения звеньев. В соответствии с величиной  будет изменяться лишь масштаб по оси времени

                                                                                                                 

Рис5. Переходная функция контура  регулирования, настроенного

на оптимум модуля передаточной функции

2. Объект с большими и малыми инерционностями первого порядка.

Если среди многих инерционных звеньев объекта есть звено, постоянная времени которого больше суммы малых постоянных времени, то следует принять меры для компенсации этой постоянной. В противном случае она будет добавляться к сумме малых постоянны времени и снижать быстродействие контура.

Так как и в этом случае, регулирование должно осуществляться практически без ошибки, регулятор должен обладать интегрирующими свойствами. Для компенсации большой постоянной времени регулятору необходимо придать еще и пропорциональные свойства.

Передаточная функция контура с ПИ-регулятором имеет вид

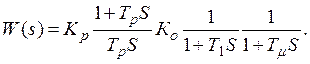
Для компенсации большой постоянной времени требуется равенство .

 

 

                

 

Рис.6 Структурная схема оптимизированного контура

При этом условии передаточная функция разомкнутого контура имеет вид

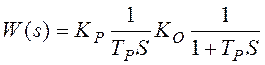, откуда для замкнутого контура имеем

.

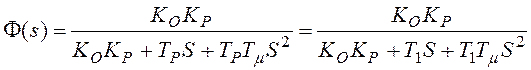Используя условие оптимизации , при       найдём значение коэффициента усиления регулятора

Подставляя полученные значения параметров в исходное уравнение, получим уравнение оптимально настроенного замкнутого контура

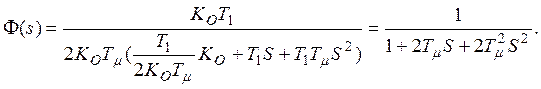
Если в цепочке инерционных звеньев первого порядка находятся две большие инерционности, то для их компенсации регулятор должен обладать двумя упреждающими (форсирующими) звеньями. Без компенсации инерционностей система будет с большим замедлением реагировать на изменение задающей величины и нейтрализовать возмущающее воздействие. В этом случае необходимо применить ПИД - регулятор   

.

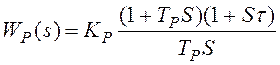Большую постоянную времени всегда необходимо компенсировать временем , а меньшую – временем .

Пример:  пусть объект регулирования содержит четыре инерционных звена с постоянными времени Т₁=400_мС,  Т₂=80_мС,  Т₃=15_мС,   Т₄=5_мС. Рассмотрим варианты оптимальных настроек контура, используя регуляторы разных типов.

 

И-регулятор           ,                                     Тр₁= 4,7=2350 _мС.

ПИ-регулятор      ,     Т_Р=Т₁=400 _мС,                   Тр₁=4,7=470 _мС

ПИД-регулятор      , Т_Р=Т₁=400 _мС,  Т_{2 мС ,}                   Тр₁= _мС.

Компенсировать третью постоянную времени с целью дальнейшего повышения быстродействия уже гораздо труднее. Для этого потребовалось бы иметь регулятор, обладающий свойствами интегрирования и двойного дифференцирования. Однако двукратное дифференцирование даже при очень малом содержании высших гармоник в колебаниях регулируемой величины приводит к такому снижению помехоустойчивости контура, что добиться стабильности регулирования в подавляющем большинстве случаев уже невозможно.

Кроме того, независимая настройка параметров такого ПИД - регулятора возможна только тогда, когда все три элемента, определяющие постоянные времени, отделены друг от друга с помощью соответствующих усилителей.

3. Объект с одной очень большой и несколькими малыми постоянными времени.

Если объект управления содержит инерционность, постоянная времени которой в 20 и более раз превосходит сумму малых постоянных времени , следует рассмотреть возможность использования  П - регулятора. Такой вариант давал бы для внешнего (подчиняющего) контура то преимущество, что его можно было бы настроить по оптимуму модуля передаточной функции. Это дает возможность иметь в уравнении высшего контура эквивалентную постоянную времени Т_Э=2. При других вариантах настройки приходится использовать ПИ-регулятор и настраивать его по правилам симметричного оптимума, что снижает быстродействие внешнего контура примерно в 2 раза.