По
окончании переходного процесса в обоих случаях происходит интегрирование,
соответствующее параметрам применённого регулятора, т.е. крутизна нарастания
регулируемой величины в обоих случаях одинакова. Точно также одинаков и
временной сдвиг, равный ![]() В случае одной инерционности начальная часть
переходного процесса происходит более плавно и длится дольше. С увеличением
числа инерционных звеньев выходная величина на начальном участке все теснее
прилегает к оси абсцисс; при бесконечно большом числе звеньев она оставалась бы
полностью на оси абсцисс вплоть до момента времени
В случае одной инерционности начальная часть
переходного процесса происходит более плавно и длится дольше. С увеличением
числа инерционных звеньев выходная величина на начальном участке все теснее
прилегает к оси абсцисс; при бесконечно большом числе звеньев она оставалась бы
полностью на оси абсцисс вплоть до момента времени ![]() ,
когда она претерпевала бы излом и переходила в сдвинутую по времени прямую
интегрирования. Именно такой вид характерен для звена с запаздыванием (рис.4).
,
когда она претерпевала бы излом и переходила в сдвинутую по времени прямую
интегрирования. Именно такой вид характерен для звена с запаздыванием (рис.4).
Выводы:
1.Последовательное соединение
большого числа инерционных звеньев без существенного ущерба для точности можно
заменить одним инерционным звеном, постоянная времени которого ![]() равна сумме постоянных времени исходных звеньев. При
этом необходимо, чтобы в рассматриваемом контуре имелось по крайней мере одно
интегрирующее звено или одно инерционное звено с постоянной времени во много
раз большей, чем сумма малых постоянных времени. Последнее основывается на
сходстве, существующем между интегрирующем и инерционным звеньями, вытекающем
из следующих рассуждений.
равна сумме постоянных времени исходных звеньев. При
этом необходимо, чтобы в рассматриваемом контуре имелось по крайней мере одно
интегрирующее звено или одно инерционное звено с постоянной времени во много
раз большей, чем сумма малых постоянных времени. Последнее основывается на
сходстве, существующем между интегрирующем и инерционным звеньями, вытекающем
из следующих рассуждений.
1.Передаточная функция инерционного звена
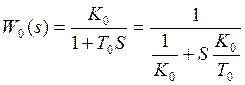 .
.
Если устремить К0
инерционного звена к бесконечности, но при этом потребовать чтобы дробь![]() оставалась конечной, то получим
оставалась конечной, то получим 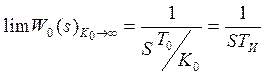 , т.е. инерционное звено
первого порядка переходит в интегрирующее.
, т.е. инерционное звено
первого порядка переходит в интегрирующее.



![]()
![]()
 y
y
y
y
 |
А) Б)
![]()
![]() t
t
t
t
![]()
![]()
![]()
![]()
Рис.4. Реакция последовательно соединённых большой и многих малых инерционностей первого порядка – А и последовательно соединенных интегрирующего и запаздывающего звеньев Б.
2.При
сформулированных выше условиях, путем перехода к бесконечно большому числу
малых постоянных времени с неизменной суммой ![]() , звено запаздывания можно представить также в виде
инерционного звена первого порядка.
, звено запаздывания можно представить также в виде
инерционного звена первого порядка.
На основании изложенного передаточную функцию контура можно записать в виде
![]()
откуда передаточная функция замкнутого контура будет иметь вид
![]() .
.
Оптимум по модулю передаточной функции
(модульный оптимум)
Этот вариант оптимизации рассматривается на ряде типовых примеров, охватывающих все практические случаи применения подобных способов настройки.
1.Объект со многими малыми инерционностями первого порядка.
Если объект управления не содержит интегрирующих звеньев, можно провести оптимизацию модуля передаточной функции контура регулирования, используя
И - регулятор.
Оптимизация состоит в пригонке модуля к единице для возможно более широкой полосы частот.
Передаточная функция замкнутого контура
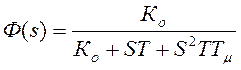 , для пригонки модуля
передаточной функции к единице следует использовать первое условие оптимизации
, для пригонки модуля
передаточной функции к единице следует использовать первое условие оптимизации ![]() ,
которое при
,
которое при ![]() дает следующее значение оптимальных параметров
регулятора:
дает следующее значение оптимальных параметров
регулятора:
для И -регулятора
![]()
Передаточная функция приобретает вид
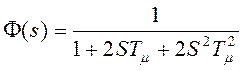 .
.
Следовательно, передаточная функция оптимизированного контура определятся только суммой малых постоянных времени. Это должно быть справедливо и для переходной функции оптимизированного контура регулирования. Так как полином знаменателя всегда соответствует однородному дифференциальному уравнению переходного процесса, то можно написать
![]()
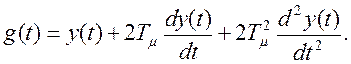
Сопоставив это
уравнение с нормированным уравнением второго порядка, для постоянной времени и
относительного коэффициента демпфирования ![]() имеем:
имеем:
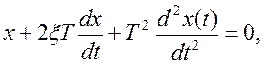
![]()
![]() .
.![]()
Так как ![]() , то переходная функция будет описываться уравнением
, то переходная функция будет описываться уравнением
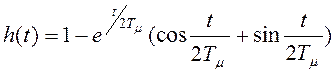 .
.![]()
![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.