Нелинейные системы автоматического управления (НСАУ). Особенности математических моделей НСАУ. Разновидности структур и звеньев в НСАУ

Нелинейные системы автоматического управления (НСАУ)

Введение

В. 1. Исходные сведения

К НСАУ  относятся все технические устройства с обратной связью, математические модели которых описываются неоднородными нелинейными дифференциальными уравнениями. В компактной форме неоднородное линейное дифференциальное уравнение может быть представлено выражением:

, где  и  - операторные полиномы, p=d/dt– символ операции дифференцирования, а  и  - переменные-координаты "выхода" и "входа" системы.

Представленное выражение обычно получают на основании системы  неоднородных линейных дифференциальных уравнений от нулевого до второго порядка. В ней "выходами" и "входами" будут промежуточные (внутренние) переменные. Такая система уравнений составляется с учетом принятого представления о математических моделях всех элементов, составляющих данную линейную САУ, и информационных связей между ними, то есть по структурной схеме САУ.

Система, в математической модели которой все коэффициенты а_iи b_jполиномовQ(p) и R(p) есть постоянные величины, называется стационарной. В случае переменных (во времени) коэффициентов система называется нестациаонарной. Если значение одного или части коэффициентов а_i, b_jзависят от величины какой либо переменной САУ, такая система называется нелинейной. Чаще всего такой переменной является рассогласование e(t). Если функцией e(t) станет  коэффициент передачи безинерционного звена, то в модели САУ появится нелинейное статическое звено (статическая нелинейность). Обобщенный символ  статической нелинейности F(x):

В НСАУ встречаются и нелинейные динамические звенья (динамические нелинейности). Их физическая природа может быть связана с наличием зависимости постоянной времени (динамического параметра) какого либо звена модели системы а_iили b_j от переменной (координаты). Если в теории линейных систем поведение систем изучается при малых отклонениях переменных Δx(t), Δg(t), Δe(t) и т. д., то можно было считать и динамические параметры системы неизменными. Однако в НСАУ отклонения переменных определяются реальными условиями их работы. Например, на рис. ниже изображены характеристики намагничивания ротора (якоря) электромашины (или иного электромагнитного устройства).

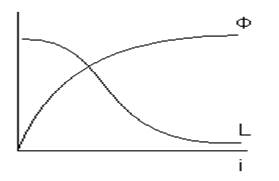
Динамический параметр модели устройства  - электромагнитная постоянная времени апериодического звена . Если входной переменной такого звена является ток намагничивания i, то характеристика динамической нелинейности будет F(i, pi).

Резюме. В математической модели НСАУ имеются звенья с разнообразными статическими или динамическими нелинейностями. Поэтому для описания её структуры нельзя использовать переместительный (коммутативный) и сочетательный (ассоциативный) законы линейной математики. Следовательно, нельзя представить компактную единую форму записи для неоднородного нелинейного дифференциального уравнения любого порядка.

Таким образом,математическая  модель НСАУ может быть представлена только в виде соединения различных подсистем, содержащих линейную часть (ЛЧ) с записью её модели в линейной операторной форме и нелинейную часть (НЧ) с записью её модели в нелинейной форме  (нелинейных алгебраических или (и) нелинейных дифференциальных уравнений).

Аналитически, для нелинейной подсистемы, где последовательно соединены линейная и нелинейная части:

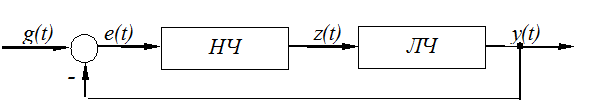
математическая модель имеет вид:

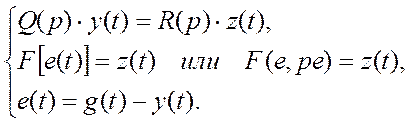
Нелинейная части подсистемы может быть представлена в табличной или графической форме.

В этом частном случае замкнутая НСАУ содержит одну ЛЧ и одну НЧ, но может быть и множество других комбинаций. Поэтому структуры  НСАУ в общем случае подразделяются на классы.

В реальной системе НЧ часто представляется одним нелинейным элементом (НЭ) (реле, умножителем, делителем и т. п. устройством). Поэтому в функциональных схемах НСАУ используют и такую аббривиатуру - НЭ.

          Параметры нелинейных САУ не зависят от времени. Не следует путать стационарные НСАУ с нестационарными системами.

В. 2. Особенности математических моделей НСАУ

1. Поскольку для формирования математических моделей НСАУ нельзя использовать большинство законов линейной алгебры, то в них не соблюдаются: принцип суперпозиции, "правила предельного перехода" для определения начальных и конечных значений функций, многие правила преобразования структур, а также многие методы исследования ЛСАУ.

Критерии устойчивости ЛСАУ не приемлемы для НСАУ. При анализе движений нелинейных систем можно говорить лишь об устойчивости отдельных её динамических процессов или об устойчивости динамики системы.

Много различий в методах анализа и синтеза линейных и нелинейных САУ.

2.Исходя из понимания формул и содержания В.1 становится очевидным, что теория НСАУ не может содержать общих решений поставленных задач, то есть нет (и не может быть) общих решений устойчивости, синтеза и анализа НСАУ.

3. Следовательно, теория НСАУ состоит из набора решений задач устойчивости, анализа и синтеза для отдельных (частных) структур нелинейных систем. В этом состоит первая сложность её изучения.При изучении теории НСАУ нужно грамотно решить: возможно ли применение того или иного решения (метода) к конкретно поставленной задаче (модели)? В этом состоит вторая сложность изучениятеории НСАУ.