Нелинейные системы автоматического управления (НСАУ). Особенности математических моделей НСАУ. Разновидности структур и звеньев в НСАУ, страница 6

Пусть в системе, аналогичной предыдущей, обратная связь положительна.   Тогда в  замкнутой системе после ввода обратных операторов получается:

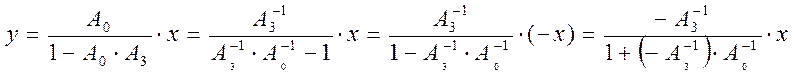, что соответствует следующим структурным схемам:

                

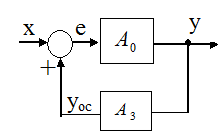
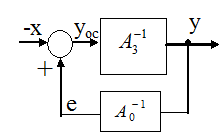
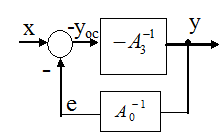
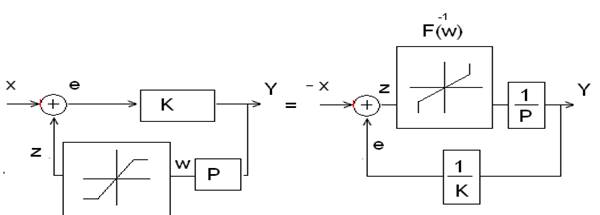
Правая схема - это система с отрицательной обратной связью, в прямом канале которой находится обратный оператор цепи обратной связи исходной системы, взятый с противоположным знаком.

Таким образом:     .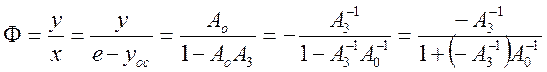

Правило 6

В структурных схемах, представляющих собою замкнутый контур с отрицательной (положительной) обратной связью, можно оператор в прямой цепи заменить обратным оператором цепи обратной связи, а оператор обратной связи заменить обратным оператором прямой цепи. Тогда оператор замкнутого контура при наличии отрицательной связиможет быть найден по формуле 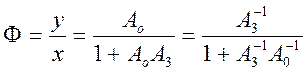, а приположительной связи- по формуле  .

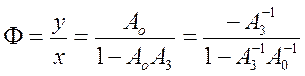Пример:

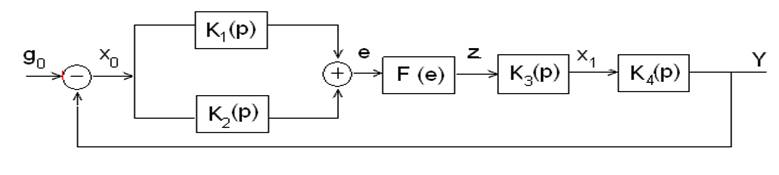
1.Задана нелинейная структура, изображенная на рисунке. В какой форме её целесообразнее исследовать: в прямой или с помощью "обратных операторов" отдельных звеньев?

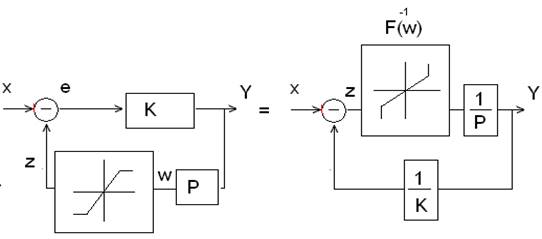
По левой схеме можно записать такое выражение для оператора блока:

.

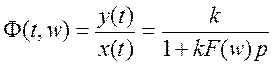По правой схеме записывается равнозначная зависимость:

.

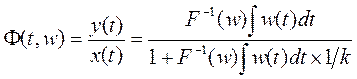В обеих схемах  - оператор дифференцирования, поэтому:  и .

Тогда, если заменить нелинейность F(w) линейным звеном с коэффициентом передачи , легко представить оператор левой замкнутой системы в виде: 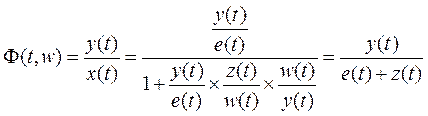    (очень простое выражение).

Чем же не устраивает левая структура, что хотят выполнить ее преобразование с использованием обратных операторов? Дело в том, что в реальных условиях работы сигнал управления x(t) всегда "зашумлен" помехами, которые могут сильно исказить заданные характеристики САУ.

Пусть x(t)=x_o(t)+x_n(t), где x_o(t) сигнал задания,  x_n(t) помеха. Оба этих сигнала переходят в прямой канал в виде: x_o(t)+x_n(t)-z_o(t)=e_o(t)+x_n(t). (Здесь предполагается, что сигнал обратной связи помехой не искажен).  Итак, полезный сигнал, приняв значение e_o(t), существенно уменьшился, а помеха x_n(t) не изменилась. На выходе системы получили y(t) = k(e_o(t)+x_n(t)) = y_o(t)+y_n(t), причем, вторая составляющая может превышать первую. Эти же две составляющие сигнала поступают в цепь обратной связи. В силу различия спектрального состава они различным образом дифференцируются и, следовательно, по разному обрабатываются нелинейностью.

Чем же лучше будет правая структура? Во первых, в прямой канал поступает сигнал x_o(t)+x_n(t)-e_o(t)=z_o(t)+x_n(t). Составляющая управления z_o(t) здесь много больше помехи.

При интегрировании w_o(t) восстанавливается полезный сигнал y_o(t), а сигнал помехи , так  как помеха обычно высокочастотна с малой постоянной составляющей. В цепи обратной связи помеха еще более ослабляется в "k" раз, а полезный сигнал y_o(t) ослабляется до нужного значения e_o(t).

2. Таким же образом можно заменять и структуры с положительной обратной связью.

Однако замыкание контуров положительной обратной связью часто приводит к их структурной неустойчивости. Такие преобразования, даже в моделях НСАУ, используют крайне редко. Поэтому не стоит подробно оценивать их свойства.

Очень важно знать и помнить, что правило 6 можно применять только для структур, не содержащих звеньев "направленного (одностороннего) действия". Большинство же электронных устройств (релейные и аналоговые усилители, компараторы, преобразователи частоты и напряжения) - элементы направленного действия. Тогда правило 6 просто физически не реализуемо.

Изображение моделей НСАУ с помощью направленных графов

Теория направленных графов может быть использована для представления и преобразования структурных схем  НСАУ.

Например, в изображенной ниже схеме, - линейные операторы, - нелинейность (нелинейный оператор).

В направленных графах есть только два элемента: "узел" и "ветвь", образующие "дерево графа".

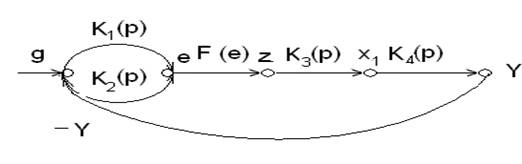
На рисунке изображено дерево графа, полученное на основании преобразования структурной схемы. Здесь все переменные модели  представляют собою узлы, причем g_oисток, Yсток, остальные узлы  - промежуточные (каскадные).

1. Узел x_o  имеет уравнение: , а узел  .

2. Исключим каскадный узел и две параллельные ветви:

,    .

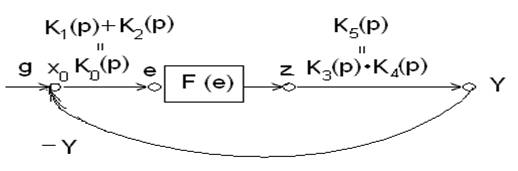
3. Отделим узел Y, и получим структуру:

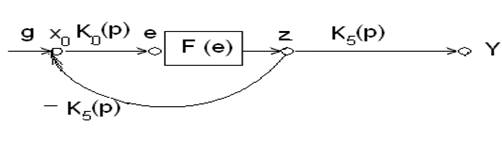
4. Далее решение задачи сводится к приведению полученной структуры к моделям НСАУ одного из трех классов.