Нелинейные системы автоматического управления (НСАУ). Особенности математических моделей НСАУ. Разновидности структур и звеньев в НСАУ, страница 5

Например, нечетно-симметричное звено с зоной нечувствительности и насыщением описывается:

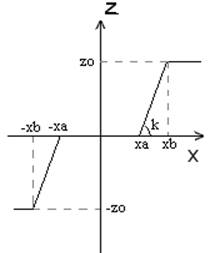
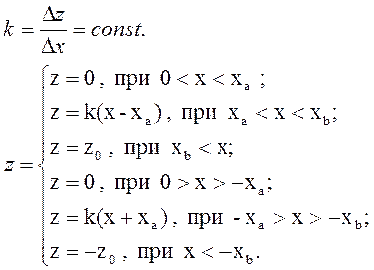
А с использованием кусочно-линейного оператора его математическая модель будет иметь вид:

.

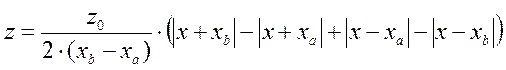Математические модели звеньев с неоднозначными характеристиками уже являются не статическими, а динамическим. В выражениях для их описания используются производные входной величины или конечные разности. Наиболее удобно эти звенья представляются разностными уравнениями.

Особенности структурных преобразований в НСАУ

Общие положения

В моделях ЛСАУ для аналитического определения (расчета) их статических и динамических характеристик используют математический аппарат линейных дифференциальных и алгебраических уравнений. Тогда все исследования выполняются во временной области, где оперируют с непрерывными функциями вещественного аргумента -  времени. При этом описание моделей выполняется по принципу "вход - выход", когда координата выхода y(t) находится как реакция системы на приложенное к её входу известное управляющее воздействие g(t). Возможно математическое описание модели САУ "в пространстве  состояний", то есть в матричной форме в виде функции от переменных состояния(то есть от всех координат системы), которые составляют матрицу-столбец.

Второй способ связан с использованием преобразования Лапласа для всех линейных уравнений и переменных модели. При этом модели САУ "вход - выход" "переписываются" в виде передаточных функций, а аргумент становится комплексной величиной: вида s=α+jω, размерности рад/с (1/с).

Очевидно и преобразованные по Лапласу функции y(s) или g(s) становятся комплексно-значимыми и изображаются  в комплексной плоскости. В большинстве практических применений преобразования Лапласа принимают s=jω. Тогда аргумент становится угловой частотой, а все функции - частотными.Поэтому важно понимать идентичность временных и частотных характеристик  моделей линейных САУ. Простота и трудоёмкость методов выполнения поставленной задачи являются главными признаками выбора временной или частотной областей её решений.

Итак, при описании ЛСАУ используется  передаточная функция: 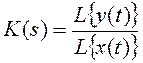. В НСАУ вводится в рассмотрение "оператор преобразования" или "оператор передач" .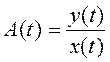

Если при последовательном соединении звеньев , то обратная передаточная функция в модели ЛСАУ принимает вид: . А вот в модели НСАУ при , запись  может быть правильной, а  является неверной. Переместительный закон в случае нелинейных систем несправедлив!!!!

Пример:   Пусть НЭ и ЛЧ соединены последовательно:

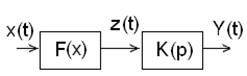,    где 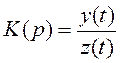,   тогда  .

Для данного примера обратное преобразование получается "при движении" от выхода ко входу:  .

Основные преобразования структурных схем НСАУ

В моделях ЛСАУ используется 5 основных дуальных правил преобразований структурных схем:

1.  Перенос точки ветвления (сумматора) через точку ветвления (сумматор).

2.  Перенос сумматора (точки ветвления) через точку ветвления (сумматор) (в направлении передачи информации и против направления передачи информации).

3.  Перенос точки ветвления через звено (с учетом направлений переноса).

4.  Перенос сумматора через звено (с учетом направлений переноса).

5.  Перенос звена через звено (с учетом направлений переноса).

В структурных схемах НСАУ правила 1 и 2 работают без ограничений, так как в этих комбинациях нет нелинейностей.

Правило 3 можно применять при переносе точки ветвления только в линейной части (ЛЧ) схемы.

Правило 4 нельзя применять, так как в моделях НСАУ не работает принцип суперпозиции.

Правило 5 использовать нельзя, так как переместительный закон в этих структурах не действует.

Поэтому для преобразования структур НСАУ используют правило 6, которое пригодно и для структурных схем ЛСАУ, (но там редко используется ввиду ненадобности).

Шестое правило преобразования структурных схем

Рассмотрим замкнутую нелинейную систему с отрицательной обратной связью. Её модель изображена ниже на рисунке. Операторы: прямой (основной) цепи  и цепи обратной связи . На основании очевидного равенства 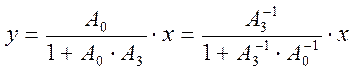, найденного делением всех слагаемых числителя и знаменателя на бесспорную информационную последовательность , получили выражение:  

.

                

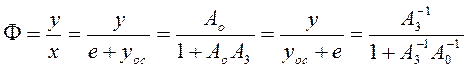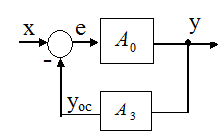
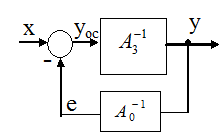
Здесь  в левой схеме x = e + y_oc, и в правой схеме x = y_oc + e  - тождественные преобразования информации на  входах систем.