Нелинейные системы автоматического управления (НСАУ). Особенности математических моделей НСАУ. Разновидности структур и звеньев в НСАУ, страница 4

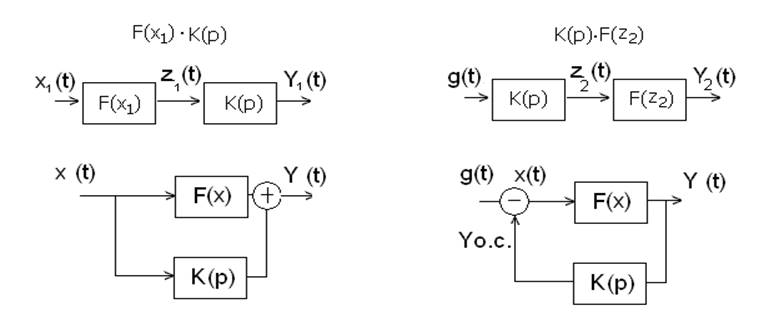
На рис. изображено четыре варианта соединения линейных и нелинейных звеньев, естественно, их может быть больше.

1). Схема с последовательным включением нелинейного элемента и ЛЧ неразрешима, если полученная на выходе нелинейности функция  нелинейная и не может быть заменена эквивалентным линейным функционалом.

2). Схема с последовательным включением ЛЧ и нелинейностью легко разрешима, так как полученная на выходе ЛЧ линейная функция  подвергается лишь нелинейному безинерционному масштабированию элементом F(z₂).

3) Схема с параллельным соединением линейного и нелинейного элементов не вызывает проблем, так как выходная величина ЛЧ складывается с сигналом безинерционного НЭ.

Подобные правила можно применить и для анализа других разомкнутыхсистем. Сложнее аналитически исследовать замкнутые системы.

4). Схема с отрицательной обратной связью.

Пусть F(x) будет статическая, гладкая, нечетно-симметричная зависимость, а обратная связь реализуется безинерционным линейным звеном с коэффициентом передачи k (К(р)= k). Поэтому уравнение  алгебраическое (не дифференциальное!). Если сигнал g известен, то можно получить зависимость F(g).

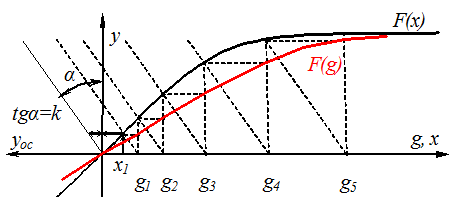
Задача может быть решена графо-аналитическим способом. Сначала равенство  записывается в виде g=x+y_oc,  где . Тогда, задавая последовательно ряд значений x_i и, решая графически уравнение  g=x+y_oc, получим искомую нелинейность F(g). ("Красная" кривая на рис.).

Вспомогательная прямая, как решение уравнения , построена во втором квадранте.

Опишем алгоритм решения задачи при x = x₁ . На кривой F(x)=y при x = x₁ получили значение F(x₁) = y₁  - (ближняя точка на кривой от начала координат). Из точки y₁ провели прямую, характеризующую уравнение обратной связи, до оси абсцисс. Получили решение уравнения g=x+y_oc в виде g₁=x₁+y_oc1. По ординатам g₁ и y₁ нашли первую точку "красной" кривой F(g). Далее, принимая x₂= g₁, находим y₂ и повторяем решение задачи.

Охват нелинейности отрицательной обратной связью всегда приводит к расширению зоны линейности её характеристики. Этим свойством линейной отрицательной обратной связи часто пользуются в реальных механизмах и устройствах для уменьшения влияния естественных нелинейностей их узлов и деталей на динамические и установившиеся режимы работы

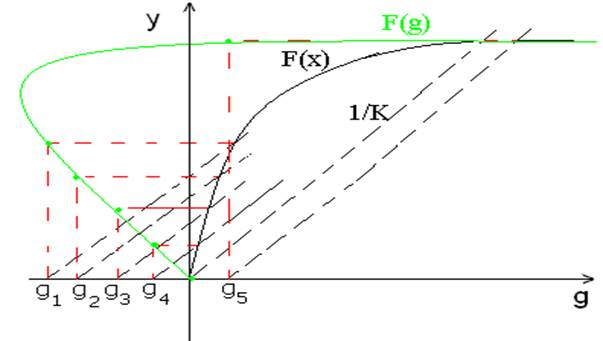
4). Рассмотрим влияние охвата нелинейности положительной обратной связью. Характеристика нелинейности F(x) та же, что и в предыдущем примере, но теперь , а  Методика построения "зеленой" кривой F(g) аналогична. Как следует из рисунка ниже, характеристика замкнутой системы F(g) стала более нелинейной и даже "статически неустойчивой"  на участке изменения сигнала управления g от 0 до значения g₄ , а при значении сигнала g₅ характеристика нелинейности F(g) входит в зону насыщения. Реально нелинейность F(x) приобрела физические свойства "однополярного реле" F(g).

Особые нелинейные звенья

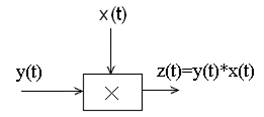
Особыми нелинейными звеньями являются:  умножители, делители, квадраторы, радикалы, тригонометрические функторы и другие…

(

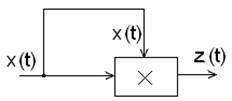
Рассмотрим пример работы с блоком умножения.

                                      

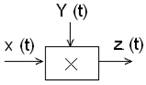
          а). Пусть x(t)=x₀ =const. Перейдем к линейным  преобразованиям (Лапласа): 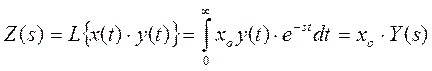 . Если функция y(t) удовлетворяет условиям преобразования Лапласа (самое важное из которых: y(t)=0 при ,   - ограниченного роста при t > 0). Следовательно, преобразование Лапласа для произведения  возможно, иными словами нелинейное звено выродилось в линейное.

б) Если , а x(t) удовлетворяет условиям Лапласа, то также нелинейного звена нет.

в) Если :

 

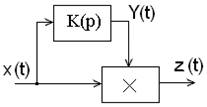
Получаем - явно нелинейный сигнал, то есть на выходе блока умножения имеет место нелинейная функция z(t), определяющая динамику системы.

г) Если , тогда Z(t)=x²(t) нелинейная квадратичная функция. Аналогично, произведение  также нелинейная функция.

                          

Математические модели нелинейных звеньев

Нелинейные звенья звеньев с однозначными характеристиками могут быть описаны аналитическими зависимостями (в случае гладких нелинейностей). Для упрощения выражений рекомендуется использовать аппроксимацию. В том случае, если характеристика звена есть ломаная линия (кусочно-линейные звенья), то его математическая модель представляется арифметико-логической функций или кусочно-линейным оператором.