Пусть
многочлен f(x)
задается формулой (27). Тогда ![]()
![]() , что и требовалось доказать.
, что и требовалось доказать.
Свойство 2. Производная суммы нескольких многочленов равна сумме их производных.
Достаточно
доказать это свойство для суммы двух многочленов. Пусть ![]()
![]() ,
,
![]() . Тогда
. Тогда ![]()
![]() , где
, где ![]() , и
, и ![]()
![]()
![]()
![]() . (Как обычно, считается, что
. (Как обычно, считается, что ![]() при
при ![]() и
и ![]() при
при ![]() .)
.)
Свойство
3. Для
производной произведения двух многочленов справедлива формула ![]() .
.
Многочлен
![]() равен
сумме всевозможных произведений uv,
где u - член многочлена f(x), v -
член многочлена g(x).
Запишем это следующим образом:
равен
сумме всевозможных произведений uv,
где u - член многочлена f(x), v -
член многочлена g(x).
Запишем это следующим образом: ![]() . Согласно свойству 2 имеем:
. Согласно свойству 2 имеем: ![]() . В то же время
. В то же время ![]() и
и ![]() . Поэтому достаточно проверить,
что
. Поэтому достаточно проверить,
что ![]() для любых u, v,
т.е. доказать свойство 3 для одночленов. При этом свойство 1 позволяет свести
проверку к случаю одночленов с коэффициентами, равными единице. В этом случае
проверка производится следующим образом:
для любых u, v,
т.е. доказать свойство 3 для одночленов. При этом свойство 1 позволяет свести
проверку к случаю одночленов с коэффициентами, равными единице. В этом случае
проверка производится следующим образом: ![]() .
.
Как и в математическом анализе, из свойства 3 выводится следующая формула дифференцирования произведения любого числа множителей:
![]()
![]() .
(29)
.
(29)
Частным случаем этой формулы является формула дифференцирования степени:
![]() .
(30)
.
(30)
Таким образом, определенная нами операция дифференцирования многочленов обладает некоторыми свойствами дифференцирования функций действительной переменной[1].
Производная
от производной многочлена ![]() называется
его второй производной и обозначается через
называется
его второй производной и обозначается через ![]() . Производная от второй
производной называется третьей производной и т.д. Для n-й
производной используется обозначение
. Производная от второй
производной называется третьей производной и т.д. Для n-й
производной используется обозначение ![]() . Так как при каждом
дифференцировании степень многочлена понижается, то (n+1)-я
производная любого многочлена степени n
равна нулю.
. Так как при каждом
дифференцировании степень многочлена понижается, то (n+1)-я
производная любого многочлена степени n
равна нулю.
Схема
Горнера (см. п.2) удобна при разложении данного многочлена ![]() по степеням двучлена
по степеням двучлена ![]() . Пусть
. Пусть
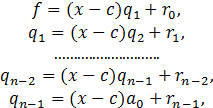 (31)
(31)
где ![]() и
и ![]() . Если последнее выражение в (31)
для
. Если последнее выражение в (31)
для ![]() подставить в предыдущее
равенство, а затем то, что при этом получится, подставить вместо
подставить в предыдущее
равенство, а затем то, что при этом получится, подставить вместо ![]() и т.д., то придем к равенству
и т.д., то придем к равенству
![]() (32)
(32)
Это есть разложение данного
полинома f по степеням (x - c).
Пусть K - поле P.
Дифференцируя обе части равенства (32) и полагая ![]() , получим
, получим ![]() ,
, ![]() ,
, ![]() ,
...,
,
..., ![]() . Поэтому равенство (32) можно
записать в виде
. Поэтому равенство (32) можно
записать в виде
![]() , если только f - полином над полем нулевой
характеристики. Это и есть формула Тейлора для полиномов. Все
вычисления удобно расположить в одну таблицу:
, если только f - полином над полем нулевой
характеристики. Это и есть формула Тейлора для полиномов. Все
вычисления удобно расположить в одну таблицу:
|
|
a0 |
a1 |
... |
an-1 |
an |
|
c |
b0 |
b1 |
... |
bn-1 |
|
|
|
c0 |
c1 |
... |
|
|
|
d0 |
d1 |
... |
|
||
|
... |
... |
... |
... |
||
|
a0 |
|
Пример
18. Разложим
полином ![]() по степеням
по степеням ![]() . Для этого
построим таблицу
. Для этого
построим таблицу
|
1 |
-5 |
0 |
3 |
0 |
0 |
-1 |
|
|
1 |
1 |
-4 |
-4 |
-1 |
-1 |
-1 |
|
|
1 |
-3 |
-7 |
-8 |
-9 |
|
||
|
1 |
-2 |
-9 |
-17 |
|
|||
|
1 |
-1 |
-10 |
|
||||
|
1 |
0 |
|
|||||
|
1 |
|
Отсюда ![]()
![]() .
.
Упражнение
15. Разложить
по степеням ![]() : 1)
: 1) ![]() ,
,
![]() ;
2)
;
2) ![]() ,
,
![]() ;
3)
;
3) ![]() ,
,
![]() ;
4)
;
4) ![]() ,
,
![]() ;
5)
;
5) ![]() ,
,
![]() ;
6)
;
6) ![]() ,
,
![]() ;
7)
;
7) ![]() ,
,
![]() ;
8)
;
8) ![]() ,
,
![]() ;
9)
;
9) ![]() ,
,
![]() ;
10)
;
10) ![]() ,
,
![]() ;
11)
;
11) ![]() ,
,
![]() ;
12)
;
12) ![]() ,
,
![]() ;
13)
;
13) ![]() ,
,
![]() ;
14)
;
14) ![]() ,
,
![]() .
.
Задача
6. Пусть f(x) –
многочлен n-й степени над R, ![]() и
и ![]() ,
, ![]() ,
…,
,
…, ![]() ,
, ![]() . Докажите, что действительные
корни многочлена f(x)
не превосходят a.
. Докажите, что действительные
корни многочлена f(x)
не превосходят a.
Как и
во всяком кольце главных идеалов, в кольце ![]() многочленов над полем P
каждый необратимый элемент может быть разложен на простые множители, причем это
разложение единственно с точностью до перестановки множителей и замены их
ассоциированными элементами.
многочленов над полем P
каждый необратимый элемент может быть разложен на простые множители, причем это
разложение единственно с точностью до перестановки множителей и замены их
ассоциированными элементами.
Напомним,
что ненулевой элемент области целостности называется простым, если он необратим
и не может быть разложен в произведение двух необратимых элементов. Простые
элементы кольца ![]() по
традиции называются неприводимыми многочленами. Поскольку необратимые
элементы кольца
по
традиции называются неприводимыми многочленами. Поскольку необратимые
элементы кольца ![]() ,
отличные от нуля, - это многочлены положительной степени, то неприводимый
многочлен - это такой многочлен положительной степени, который не может быть
разложен в произведение двух многочленов положительной степени. (Многочлен,
который может быть разложен в произведение двух многочленов положительной
степени, называется приводимым). Можно также сказать, что неприводимый
многочлен - это такой многочлен положительной степени, который не может быть
разложен в произведение двух многочленов меньшей степени. В самом деле, если в
разложении
,
отличные от нуля, - это многочлены положительной степени, то неприводимый
многочлен - это такой многочлен положительной степени, который не может быть
разложен в произведение двух многочленов положительной степени. (Многочлен,
который может быть разложен в произведение двух многочленов положительной
степени, называется приводимым). Можно также сказать, что неприводимый
многочлен - это такой многочлен положительной степени, который не может быть
разложен в произведение двух многочленов меньшей степени. В самом деле, если в
разложении ![]() оба множителя g
и h имеют положительную степень,
то каждый из них имеет степень, меньшую, чем степень f,
и обратно.
оба множителя g
и h имеют положительную степень,
то каждый из них имеет степень, меньшую, чем степень f,
и обратно.
Учитывая это определение и то, что ассоциированные многочлены отличаются только ненулевым множителем (обратимый элемент поля P), переформулируем теорему 21.
Теорема
28. Всякий
многочлен ![]() , не
являющийся элементом поля P,
может быть разложен в
произведение неприводимых многочленов:
, не
являющийся элементом поля P,
может быть разложен в
произведение неприводимых многочленов:
![]() (33)
(33)
причем если ![]() -
другое такое
разложение, то
-
другое такое
разложение, то ![]() и
при подходящей нумерации множителей имеют место равенства
и
при подходящей нумерации множителей имеют место равенства ![]() ,
, ![]() , где
, где ![]() ,
, ![]() .
.
Если
вынести за скобки старшие коэффициенты всех неприводимых множителей какого-либо
разложения многочлена ![]() ,
то многочлен f представится в виде:
,
то многочлен f представится в виде:
![]() ,
(34)
,
(34)
где ![]() - нормированные неприводимые
многочлены. Такое представление многочлена f
будем называть его нормированным разложением на неприводимые множители.
- нормированные неприводимые
многочлены. Такое представление многочлена f
будем называть его нормированным разложением на неприводимые множители.
Очевидно, что множитель a в формуле (34) совпадает со старшим коэффициентом многочлена f и что нормированное разложение на неприводимые множители единственно с точностью до перестановки множителей.
Пусть
p - какой-нибудь неприводимый
делитель многочлена ![]() .
Может случиться, что f делится не только на p,
но и на
.
Может случиться, что f делится не только на p,
но и на ![]() или даже на более высокую
степень p. Наибольшее из таких чисел k,
что f делится на
или даже на более высокую
степень p. Наибольшее из таких чисел k,
что f делится на ![]() , называется кратностью
неприводимого делителя
p многочлена f.
Иными словами, кратность равна k, если f
делится на
, называется кратностью
неприводимого делителя
p многочлена f.
Иными словами, кратность равна k, если f
делится на ![]() , но не делится на
, но не делится на ![]() . Если p
- неприводимый многочлен, не являющийся делителем многочлена
. Если p
- неприводимый многочлен, не являющийся делителем многочлена
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.