 |
 |
Как известно, подобные между собой фигуры имеют одинаковую форму (характерные углы, пропорции), но разные размеры. Часто для отыскания нужной фигуры удается действовать в два этапа: сначала воспроизвести необходимую форму, а затем достичь и требуемых размеров, изменяя масштаб чертежа. Такое «изменение масштаба» можно мыслить как преобразование плоскости, при котором все расстояния между точками в их образах изменяются в одинаковое число раз. Далее мы будем называть такое преобразование «подобием плоскости».
Определение. Подобным преобразованием плоскости (подобием) называется такое преобразование, когда любым двум точкам А1 и В1 ставятся в соответствие образы А2 и В2 из условия |A2B2| = k|A1B1| , где положительная константа k называется коэффициентом подобия.
Подобные преобразования будем обозначать буквой Р.
§ 2.1. Частные виды подобных преобразований
1) Движение (является частным случаем подобия при k = 1).
2)
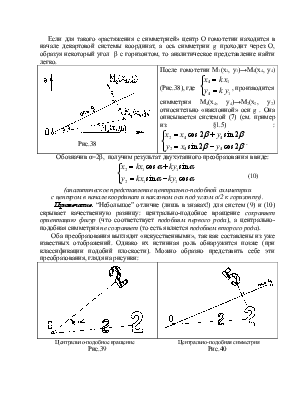
Гомотетия. Обозначение : 
.
Определение. Гомотетией с центром О и коэффициентом k называется
преобразование плоскости, при котором всякая точка А1 получает свой
образ А2 из условия 
=k
.
|
Рис.32 |
Пример. На рис.32 показаны образы А2 и B2
точек A1 и B1 при гомотетии с центром О и коэффициентом 3. Каждая точка получает свой образ на луче, выходящем из О. Точки как бы «разбегаются» во все стороны от центра, так что в результате плоскость как будто «растягивается». Если бы положительный коэффициент k был меньше единицы, то мы наблюдали бы «сжатие плоскости к центру О». |
При гомотетии неподвижной точкой является центр О .
Замечание 1. Гомотетия с коэффициентом k=1 является
тождественным преобразованием плоскости, а при k= -1
равносильна повороту вокруг центра на 180
(центральной
симметрии). Оба эти частных случая относятся к
движению.
|
Рис.33 |
Пример. На рис.33 показаны образы А2 и B2
точек A1 и B1 при гомотетии с
центром О и коэффициентом -2. При умножении вектора |
Гомотетия с коэффициентом (-k) равносильна композиции поворота (с тем же центром) на угол 180
и гомотетии с коэффициентом (k).
Замечание 2. При гомотетии образом произвольного отрезка [A1B1] будет параллельный ему отрезок [A2B2] , имеющий длину |A2B2| = k|A1B1|.
|
Рис.34 |
Доказательство. Пусть точка F
|
образ
F
точки F
принадлежит отрезку A2B2 (и делит его в
том же отношении, что и прообраз). Итак, внутренние точки отрезка A1B1
отобразились во внутренние для A2B2 , а сами
отрезки параллельны и отличаются по длине в k раз. Ч.т.д.
Следствие. Гомотетия отображает прямую - в прямую, луч - в луч.
Замечание 3. Образом произвольного треугольника при гомотетии будет подобный ему треугольник.
|
Рис.35 |
Доказательство вытекает из предыдущего замечания: стороны треугольников ∆А1В1С1 и ∆А2В2С2 (Рис.35) являются пропорциональными с общим коэффициентом k , поэтому треугольники подобны. Ч.т.д. Примечание. Треугольники не только подобны, но и «подобным образом расположены» (т.е. гомотетичны). В переводе с греческого homos – подобный , thetos – расположенный . |
Определение. Фигуру и ее образ (поточечный) при гомотетии называют гомотетично расположенными (гомотетичными).
Замечание 4. Гомотетичные фигуры подобны .
Доказательство для многоугольных фигур будет очевидным: они разбиваются на подобные треугольные фрагменты. Другие фигуры (не многоугольники) лучше рассматривать с точки зрения общего определения подобных фигур: расстояния между парами их соответственных точек должны быть пропорциональными. Это как раз характерно для гомотетии (согласно замечанию 2). Ч.т.д.
Замечание 5. Гомотетия сохраняет ориентацию фигур .
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
такое, что
= 
. Из определения гомотетии следует
=k
. Поэтому
= 
= k