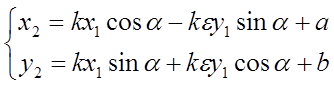Частные виды подобных преобразований плоскости. Центрально-подобное вращение. Центрально-подобная симметрия, страница 4

                                        (11)

(аналитическое представление подобного преобразования).

Примечание. Числовые параметры уравнений (11) характеризуют четыре возможных этапа подобного преобразования, переводящего произвольный треугольник в ему подобный:

1)  гомотетия (с коэффициентом  k);

2)  осевая симметрия (если она понадобится, то ε=-1, если нет, то ε=+1 );

3)  поворот (на угол α);

4)  параллельный перенос (вектор с координатами a , b).

Параметр ε  отличает подобия первого рода (ε=1)от подобий второго рода (ε=-1).

Ответу на этот вопрос посвящен следующий параграф. Попутно мы выясним, сколько всего на плоскости существует разных типов подобных преобразований. Для сравнения:  различных типов движений на плоскости всего 4 (см. таблицу 1).

§ 2.3. Классификация подобных преобразований плоскости.

Цель дальнейших рассуждений - составить для подобий «полную» таблицу, аналогичную таблице 1  для движений. Ключевым признаком для классификации удобно взять количество неподвижных точек отображения.

 

Если неподвижная точка существует, то для нахождения ее координат достаточно в уравнениях (11) «новые» координаты (х₂, у₂) заменить «старыми» (х₁, у₁),  поскольку искомая точка «перешла в себя»:    .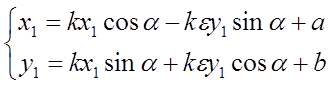

Полученную систему решим относительно х₁, у₁ , перенеся неизвестные в левую часть уравнений

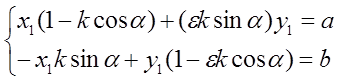                    .             (12)

Как известно, линейная система двух уравнений вида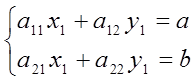        

решается (методом Крамера) путем вычисления главного определителя системы 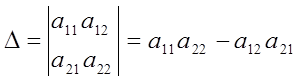                                и  двух  вспомогательных :

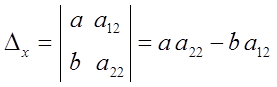       и        

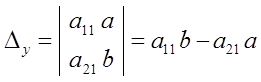
Если  ∆ ≠ 0 , то решение 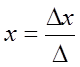   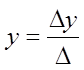,     будет единственным (а, значит, единственной будет и неподвижная точка подобного преобразования). В нашем случае a₁₁ =1- k cosα ,  a₁₂ = ε k sinα ,  a₂₁ = - k sinα , a₂₂ = 1 – ε k cosα , поэтому  ∆ = (1- k cosα)( 1 – ε k cosα) + ε k² sin²α .

Выясним, при каких условиях это выражение может обнулиться. Будем рассматривать по отдельности подобия первого рода (ε = 1) и подобия второго рода (ε = - 1).

а) Пусть ε = 1, тогда  . Сумма квадратов может обнулиться лишь в случае равенства нулю каждого слагаемого: если  ∆ = 0 , то 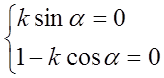  . Так как  k ≠ 0, то из  sinα = 0   следует   cosα = 1 , то есть 1k = 0,  | k | = 1 , что соответствует движению.

б) Пусть  ε = 1, тогда   .  Если  ∆ = 0 , то  k = 1 , то есть | k | = 1, что соответствует движению.

В обоих случаях (а и б) определитель системы (12) может принимать нулевое значение лишь при | k | = 1 (когда подобие оказалось движением).

Поскольку всевозможные случаи движения (| k | = 1) мы уже классифицировали (в таблице 1), постольку интерес представляют лишь подобия при | k | ≠ 1 , то есть те, которые меняют масштабы фигур при отображении. Как мы доказали, каждое такое преобразование всегда имеет ровно одну неподвижную точку.

Если совместить с этой точкой начало декартовой системы координат (наделяя ее координатами (0, 0) ), то получим для нее отображение (0, 0) → (0, 0) (в себя). Применительно к системе (11) это возможно лишь в случае, когда a = 0  и  b = 0. Значит, всякое подобие с коэффициентом  | k | ≠ 1 (то есть «не движение») в некоторой декартовой системе отсчета может иметь аналитическое представление