Математика \ Алгебра

Частные виды подобных преобразований плоскости. Центрально-подобное вращение. Центрально-подобная симметрия, страница 2

Доказательство вытекает из векторных соотношений типа  = k  (см. рассуждения к замечанию 2).    Если  k > 0 , то каждый направленный отрезок  отображается в сонаправленный ему  , а, значит, и направление поворота для произвольной пары векторов  →  (на рис.35 – против часовой стрелки) будет унаследовано их образами  → . Если же k < 0 , то такое отображение будет композицией поворота на угол 1800 и гомотетии с положительным коэффициентом, а  на каждом из этих этапов ориентация фигур сохраняется. Ч.т.д.

Аналитическое представление гомотетии с центром в начале координат

Рис.36 

Легко получить  путем рассмотрения образа  М2(х2, у2) и прообраза М1(х1, у1)    в качестве вершин подобных прямоугольных треугольников (Рис.36). Пропорция   соответственных катетов дает искомые формулы пересчета координат

                    (8)

3) Центрально-подобное вращение.  Обозначение :   .

Определение. Центрально-подобным  вращением  называют  композицию гомотетии  и  поворота  с общим для них центром.

Формулы пересчета координат точек при таком «растяжении с поворотом» легко получить для случая, когда их общим центром является начало системы координат. Тогда можно воспользоваться уравнениями гомотетии (8) и поворота (4). Пусть произвольная точка М1(х1, у1) участвует в двух преобразованиях (Рис.37).

Рис.37 

1.Гомотетия  : М1(х1, у1)→М3(х3, у3) описывается системой    .

2.Вращение : М3(х3, у3)→М2(х2, у2)

- системой                 

«Сквозная» зависимость «новых» координат от «старых» есть

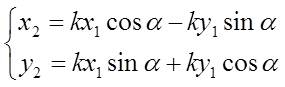                                       (9)

(аналитическое представление центрально-подобного вращения

с центром в начале координат).

4) Центрально-подобная симметрия.  Обозначение :   ,  О  g .

Определение. Центрально-подобной симметрией  называют композицию гомотетии и осевой симметрии, когда центр О гомотетии лежит на оси симметрии g .

Если для такого «растяжения с симметрией» центр О гомотетии находится в начале декартовой системы координат, а ось симметрии g проходит через О, образуя некоторый угол  β с горизонтом, то аналитическое представление найти легко.

Рис.38   

После гомотетии М1(х1, у1)→М4(х4, у4) (Рис.38), где  , производится симметрия М4(х4, у4)→М2(х2, у2) относительно «наклонной» оси g . Она описывается системой (7) (см. пример из §1.5) :    .

Обозначив α=2β,  получим результат двухэтапного преобразования в виде:                                                                            

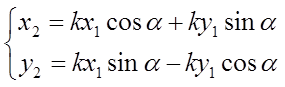                                       (10)

(аналитическое представление центрально-подобной симметрии

с центром в начале координат и наклоном оси под углом α/2 к горизонту).

         Примечание. “Небольшое” отличие (лишь в знаках!) для систем (9) и (10) скрывает качественную разницу: центрально-подобное вращение сохраняет ориентацию фигур (что соответствует подобиям первого рода), а центрально-подобная симметрия не сохраняет (то есть является подобием второго рода).

Оба преобразования выглядят «искусственными», так как составлены из уже известных отображений. Однако их истинная роль обнаружится позже (при классификации подобий плоскости). Можно образно представить себе эти преобразования, глядя на рисунки:                            

           Центрально-подобное вращение                               Центрально-подобная симметрия

                             Рис.39                                                             Рис.40

§ 2.2. Общие свойства и аналитическое представление подобий.

Скачать файл