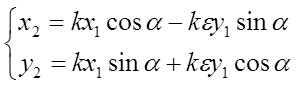 . (13)
. (13)
Заметим, что при ε = 1 (подобие первого рода) система (13) совпадает по виду с (9), то есть задает центрально-подобное вращение (Рис.39). При ε = - 1 (подобие второго рода) система (13) приобретает вид (10), то есть описывает центрально-подобную симметрию (Рис.40).
Вывод 2. Всякое подобное преобразование, изменяющее размеры фигур, является либо центрально-подобным вращением, либо центрально-подобной симметрией.
Следствие. Любое преобразование подобия, имеющее более одной или не имеющее неподвижных точек, является движением.
Эти факты положим в основу классификации, рассматривая отдельно подобия первого рода (сохраняющие ориентацию фигур) и подобия второго рода (меняющие ориентацию).
Подобия первого рода. Всевозможные преобразования будем «перебирать» по количеству их неподвижных точек. Например, если неподвижных точек 0 (нет), то, согласно следствию, это – движение. Среди движений первого рода (см. таблицу 1) неподвижных точек не имеет только параллельный перенос (это название заносим в таблицу 4).
Если неподвижная точка одна, то о коэффициенте подобия что-нибудь конкретное сказать нельзя. К выводу 1 обратное утверждение не будет справедливым: единственная неподвижная точка может иметь место как при | k | = 1 (поворот), так и при | k | ≠ 1 (центрально-подобное вращение). Впрочем, этими двумя исчерпываются все варианты (см. таблицу 1 и вывод 2). Поскольку поворот является частным случаем (при | k | = 1 ) центрально-подобного вращения, то последнее (как обобщение) и запишем в таблицу 4.
Если неподвижных точек две, то, согласно следствию, имеем движение. Но среди движений первого рода (см. таблицу 1) такими свойствами обладает лишь тождественное преобразование, а у него неподвижны и все остальные точки. Значит, в графу «количество…» заносим символ ∞ , завершая перебор.
Подобия второго рода. Если неподвижных точек 0(нет), то это – движение, а, значит (см. таблицу 1), скользящее отражение.
Если неподвижная точка одна, то таких движений второго рода не бывает, поэтому единственный вариант - «центрально-подобная симметрия».
Если неподвижных точек две, то, согласно следствию, получаем | k | = 1. Но из движений второго рода подходит лишь осевая симметрия, и то она имеет бесконечно много неподвижных точек. Записывая в таблицу 4 это название и символ ∞, тем самым завершаем перебор всех возможных подобий.
Таблица 4.
|
Род |
Количество неподвижных точек |
Коэффициент подобия K |
Название |
|
I |
0 |
|k|=1 |
Параллельный перенос,
|
|
I |
1 |
|k|=1 или |k| |
Центрально – подобное вращение,
|
|
I |
2 :
|
|k|=1 |
Тождественное преобразование, Е |
|
II |
0 |
|k|=1 |
Скользящее отражение
|
|
II |
1 |
|k| |
Центрально – подобная симметрия
|
|
II |
2 :
|
|k|=1 |
Осевая симметрия, Sl |
Вывод 3. Существует всего 6 типов подобных преобразований плоскости, из которых 4 являются движениями, и только 2 меняют размеры фигур.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.