 |
 |
Слово «affinitas» можно перевести как «родственный». В геометрии родственными называют, например, фигуру и ее параллельную проекцию на некоторую плоскость. Если движения сохраняют расстояния, подобия – пропорции фигур и углы, то аффинные преобразования сохраняют те же свойства, что и параллельная проекция.
Определение. Параллельным проектированием называют
отображение точек плоскости ω1 на точки плоскости ω2 ,
задаваемое направляющей прямой l так,
что образом всякой точки В1 
ω1
будет точка В2 ω2 ,
удовлетворяющая условию В1В2║ l.
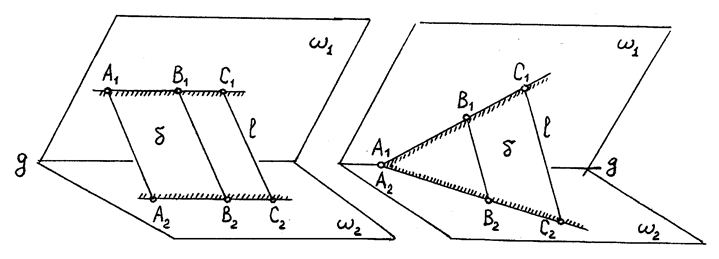
а) Рис.48 б)
Перечислим некоторые свойства параллельного проектирования:
1) Отображение
является взаимно-однозначным, то есть у каждой точки есть образ, а для каждого
образа найдется единственный прообраз. Все неподвижные точки отображения
расположены на прямой g = ω1 
ω2 (Рис.48).
2) Образом произвольной прямой В1С1 будет тоже прямая В2С2 , потому что всевозможные параллелли, проведенные через точки прямой В1С1 , окажутся в некоторой общей плоскости δ , которая рассечет ω2 тоже по прямой. Образом отрезка будет отрезок.
3) Прямая В1С1 и ее образ В2С2 либо пересекаются на прямой g (Рис.48, б), либо обе ей параллельны (Рис.48, а). В противном случае они бы скрещивались, что противоречит их общей принадлежности к плоскости δ .
4) Размеры
фигур и углы в проекциях искажаются, однако сохраняются пропорции тех отрезков,
которые лежат вдоль общей прямой. Это вытекает из теоремы Фалеса: внутри
плоскости δ на сторонах угла 
С1АС2
(Рис.48, б) параллельные прямые В1В2 и С1С2
отсекут пропорциональные отрезки: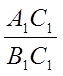 
= 
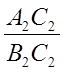(15). Иными словами, на
проекции сохранится свойство точки В делить отрезок АС в заданном отношении.
Числовая характеристика (15) будет играть далее очень важную роль, поэтому для
нее вводится специальная терминология. Дробь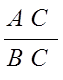 
обозначим
символически в виде скобок (АВС) (буквы перечисляются без знаков препинания).
Это число характеризует взаимное расположение трех точек общей прямой как до
отображения, так и после него. Например, зная, что (АВС)=2, можно к двум
заданным точкам А и В на прямой найти третью – С.
|
|
Впрочем, возможны два варианта расположения С (Рис.49) – внутри отрезка АВ ( С ) и вне его ( С*). |
Рис.49
Чтобы их отличить,
условимся к отношению 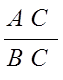добавлять знак минус,
если «третья» точка С лежит внутри отрезка АВ.
Определение. Простым отношением трех точек А, В, С одной
прямой назовем число 
= 
,
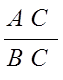где знак « – » ставится в случае, когда третья точка С лежит между двумя
первыми.
Здесь важен порядок перечисления точек, от которого зависит и число.
Пример. На рис.50 точки М, Р, К, заданные на числовой оси координатами, образуют простые отношения трех точек:
|
Рис.50 |
|
Из перечисленных свойств параллельного проектирования наиболее важными являются отображение прямой в прямую, то есть повторение в образах коллинеарного (col – общая, linear – линия) расположения точек, а также сохранение деления отрезка в заданном отношении.
Вывод. При параллельном проектировании сохраняются коллинеарность и простое отношение трех точек одной прямой.
Возвращаясь из стереометрии в планиметрию, можно теперь ввести понятие «аффинного преобразования плоскости». Речь пойдет о новом способе взаимно-однозначного отображения плоскости на себя, то есть о перераспределении точек внутри (одной!) плоскости.
Определение. Аффинным называется такое преобразование плоскости, при котором сохраняется коллинеарность и простое отношение трех точек любой прямой.
Иными словами, любые три точки А1, В1, С1 всякой прямой должны отобразиться в точки А2, В2, С2 , лежащие вместе на некоторой новой прямой, причем с сохранением отношения: (А2В2С2) = (А1В1С1).
Аффинное преобразование
обозначим буквой 
.
§ 3.1. Частные виды аффинных преобразований
1) Подобие (является частным случаем, так как сохраняет коллинеарность точек и простое отношение трех точек одной прямой).
2) Родство. Обозначение : F .
Родство можно считать неким плоским аналогом параллельного проектирования и определить наглядно с помощью фигур (Рис.48, б).
|
Рис.51 |
Повернем мысленно плоскости ω1 и ω2 вокруг общей прямой g до совмещения, чтобы все точки А1, В1, С1, … и их образы оказались в общей плоскости (Рис.51). Прямые В1В2, С1С2 в новом расположении вновь окажутся параллельными согласно обратной теореме Фалеса (если на сторонах произвольного угла соответственные отрезки пропорциональны, то отсекающие их прямые будут параллельными). |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
