|
|
Пусть их образами в силу системы (19) стали точки М(xМ,уМ),Р(хР,уР),К(хК,уК) (рис.60), что равносильно условиям хМ=а1хА+а2уА+а , yМ=b1хА+b2уА+b, хР=а1хВ+а2уВ+а , yР=b1хВ+b2уВ+b, хК=а1хС+а2уС+а , yК=b1хС+b2уС+b, которые обозначим символом (**). |
Рис.60
Докажем, что точка Р разделит
отрезок МК в том же отношении λ![]() , что и точка
В делила отрезок АС. На языке координат эта задача имеет следующий вид. Зная,
что
, что и точка
В делила отрезок АС. На языке координат эта задача имеет следующий вид. Зная,
что 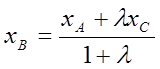 ,
, 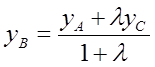 , докажем , что
, докажем , что 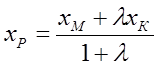 ,
, 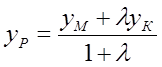 .
.
Итак, используя условия (**), получаем:
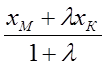 =
=
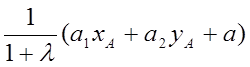
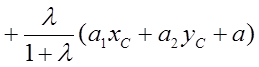 =
=
= 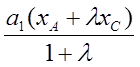 +
+
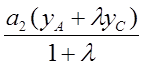 +
+ 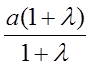 =
а1хВ+а2уВ+а
= хР .
=
а1хВ+а2уВ+а
= хР .
Поскольку для координат у
структуры всех формул аналогичны, то тем же способом получим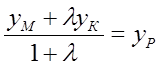 . Ч.т.д.
. Ч.т.д.
Замечание 3. Аналитические представления всевозможных подобий и движений являются частными случаями системы (19).
§ 3.4. Аффинные свойства фигур и их применение к решению задач планиметрии.
Аффинными называют свойства и понятия, которые сохраняют свой смысл после любого аффинного преобразования (например, родства), а, значит, и после параллельного проектирования.
Примеры. К аффинным понятиям относятся «прямая», «отрезок», «параллелограмм», «треугольник», «медиана» и т.п. Не являются аффинными термины «квадрат» (его образом может стать не квадрат), «высота треугольника» (так как углы при аффинном отображении искажаются) и.т.д.
Аффинными свойствами являются «параллельность», «деление отрезка в заданном отношении», «численное отношение площадей фигур» (см. доказательства в §3.2) и.т.д.
В некоторых школьных задачниках по геометрии выделяют даже разделы под названием «аффинные задачи». Их характерным признаком является употребление в текстах задач только аффинных понятий и свойств. Покажем решение такого рода задач с применением аффинных преобразований.
Задача 1. Доказать, что в произвольной трапеции прямая, проведенная через точку пересечения диагоналей и через точку пересечения продолжений боковых сторон, делит основания пополам.
Доказательство. Произвольная трапеция АВСD является частью треугольника АFD (рис.61, а). Нужно доказать, что прямая FO рассекает пополам отрезки АD и ВС. Согласно теореме из §3.2, найдется аффинное преобразование, отображающее ∆АFD в наперед заданный , например, равнобедренный ∆А1F1D1 (рис.61, б).
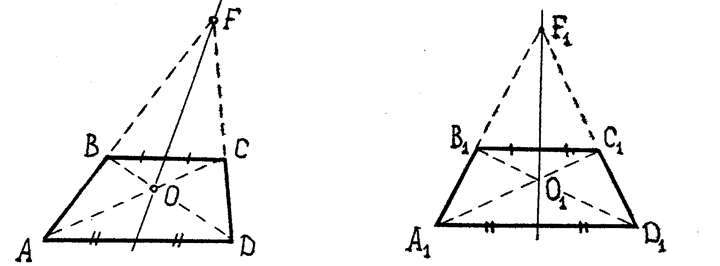
а) Рис.61 б)
Его частью станет трапеция А1В1С1D1 , т.к. сохранится параллельность прямых. Сохранятся также отношения, в которых точки В и С делят боковые стороны АF и FD. Новая трапеция станет равнобедренной, поэтому (из условий симметрии) ее основания разделятся прямой F1O1 пополам. Подвергнем ∆А1F1D1 обратному преобразованию, отображая его в ∆АFD . Отрезки А1D1 и В1С1 перейдут в основания исходной трапеции, причем сохранится свойство их деления пополам прямой FO . Ч.т.д.
Примечание. Рассмотренная задача является «чисто аффинной», так как в тексте ее условия употребляются только аффинные свойства и понятия: «трапеция», «прямая», «пересечение», «деление отрезка пополам». Равнобедренная трапеция А1В1С1D1 может служить образом исходной АВСD, поэтому любое аффинное свойство одной должно встретиться и у другой. Идея решения состояла в том, чтобы из всех «аффинно-эквивалентных» между собой трапеций выбрать ту, для которой доказываемое свойство наиболее очевидно.
Задача 2. На сторонах произвольного ∆АВС выбраны последовательно точки M, P, L так, что стороны разделены ими в отношениях k1 , k2 , k3 . Доказать, что площадь ∆MPL не зависит от того, на какой из сторон выбрана точка М.
Доказательство. Поскольку площадь ∆АВС заранее определена, то речь можно вести о той доле площади, которую от «целого» составит ∆MPL . Отношение площадей не изменится при любом аффинном преобразовании (см. замечание 4 из §3.2), как и деление сторон треугольника в отношениях k1 , k2 , k3 . Используем аффинное преобразование, переводящее заданный ∆АВС в равносторонний ∆А1В1С1 (рис.62 а, б).
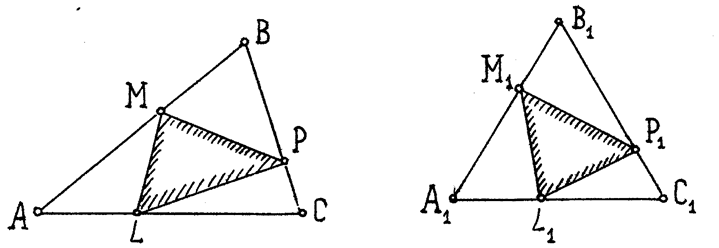
а) Рис. 62 б)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.