Аффинные преобразования плоскости. Некоторые свойства параллельного проектирования. Частные виды аффинных преобразований, страница 5

Итак, конкретное аффинное преобразование плоскости можно задать путем предъявления двух произвольных треугольников (как прообраз и образ). Пусть это будут те же  ∆А₁В₁С₁  и  ∆А₂В₂С₂ , что и на рис.58. Введем декартову координатную систему с центром в точке А₁, направляя ось  х  вдоль отрезка А₁С₁ (рис.59). Пусть для заданной произвольной точки М₁(х₁, y₁) образом окажется  точка М₂(х₂, y₂).

Будем искать зависимость между их координатами, считая аффинное преобразование «разложенным» на две компоненты: А = Р  F (см. доказательство теоремы в §3.2). На каждом этапе отображения будем “пересчитывать” координаты образа.

Рис.59

1) Родство  F : ∆А₁В₁С₁   →  ∆А₁В₃С₁  даст для точки М₁(х₁, y₁) некоторый «промежуточный» образ М₃(х₃, y₃). Расположение оси  х  вдоль оси А₁С₁  родства позволяет применить уравнения вида (17):

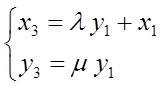
2) Подобие  Р : ∆А₁В₃С₁   →  ∆А₂В₂С₂  отобразит  М₃(х₃, y₃) в точку М₂(х₂, y₂), причем расположение координатных осей по отношению к треугольникам является таким же (рис.42), как и при выводе системы  аналитического представления подобия (11). Поэтому получим

      .

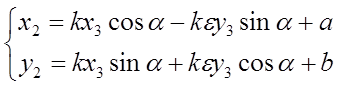Сочетая эти системы уравнений, можно найти сквозь два этапа преобразований искомую зависимость между координатами в виде

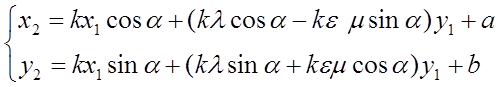             (18)

Обилие числовых параметров в уравнениях напоминает нам о представлении подобия в виде композиции гомотетии (коэффициент k) и движения, которое, в свою очередь, «распадалось» на осевую симметрию (если она понадобилась, то берем ε=-1, если нет, то ε=1), поворот (на угол α) и параллельный перенос (с координатами a, b).             Иначе говоря, более «подробным» представлением аффинного преобразования, переводящего заданные  ∆А₁В₁С₁  в    ∆А₂В₂С₂ , будет                     

 .

В новых обозначениях  а₁= kcosα ,  a₂ = kλcosα – kεμsinα  , b₁=ksinα ,   b₂=kλsinα + kεμcosαсистема  (18)  превращается в

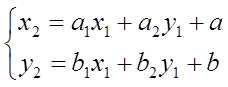                        (19)

(аналитическое представление аффинного преобразования).

Определитель этой системы не равен нулю:    

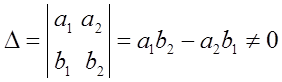       (20)

Действительно, после упрощения выражения

∆ = k cosα (λksinα + εkμcosα) - ksinα (λkcosα - εkμsinα)

получим  значение  ∆ = k²εμ . Оно не может «обнулиться», поскольку  k ≠ 0 (коэффициент гомотетии),  ε = 1,   μ = m₁/m₂ ≠ 0, так как точка В₁(q₁, m₁) (одна из двух, задававших преобразование родства) не лежит на оси родства, то есть  m₁ ≠ 0 .

Невырожденность (20) означает возможность обращения матрицы системы  (19), то есть получения обратной зависимости «старых» координат от «новых» в некотором виде 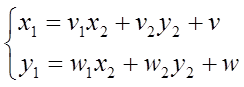(21):

                             (21)

Это обратное преобразование будет, в частности, отображать «второй» треугольник     ∆А₂В₂С₂  в “первый”   ∆А₁В₁С₁. 

Рассмотрим теперь утверждение, обратное к замечанию 1.

Доказательство. Покажем, что отображение точек плоскости по правилам (19)-(20) будет удовлетворять определению аффинного преобразования, то есть сохранит в образах коллинеарность и простое отношение трех точек прямой.

1)  Коллинеарность сохранится, если любая прямая перейдет снова в прямую. Любая прямая на плоскости задается некоторым уравнением   Ах + Вy + С = 0 .    Пусть точка с координатами х₁ , у₁ , принадлежащая этой прямой (т.е.  Ах₁ + Вy₁ + С = 0), отобразилась в  х₂, у₂  . Используя обратное преобразование (21), получим А(v₁x₂+v₂y₂+v)+B(w₁x₂+w₂y₂+w)+C=0, что в обозначениях Av₁+Bw₁=A^* , Av₂+Dw₂=B^* , Av+Bw+C=C^* равносильно условию A^*x₂+B^*y₂+C^*=0  принадлежности образов к новой прямой. Итак, прямая отобразилась в прямую. Ч.т.д.

2)  Сохранение простого отношения проверяем для произвольных трех точек А(х_А, у_А), В(х_В, у_В), С(х_С, у_С) одной прямой.