4) Применение композиций простейших движений
В §1.5 мы использовали композиции двух осевых симметрий, заменяя ими, при необходимости, поворот или параллельный перенос. Это упрощало рассуждения и позволяло решать частные задачи (например, вывести уравнения (7)). Другое применение композиции движений (а именно, поворотов плоскости) было показано в самой первой задаче во введении (рис. на обложке). В ней применялся прием, который условно назовем «методом неподвижной точки».
Схема «метода неподвижной точки»:
а) выявлено некоторое движение (или композиция движений), в результате которого имеется неподвижная точка; то есть характер движения известен и известно, какова неподвижная точка (даже если она пока не построена);
б) берется произвольно точка F1 и строится ее образ F2 при этом движении. По точкам F1 и F2 восстанавливается неподвижная точка плоскости.
Пример. Построить пятиугольник, если на плоскости указаны лишь середины М1, М2,М3, М4, М5 его сторон.
Анализ. Рассмотрим композицию пяти поворотов на 1800 вокруг центров М1, М2, М3, М4, М5 (Рис.30, а).
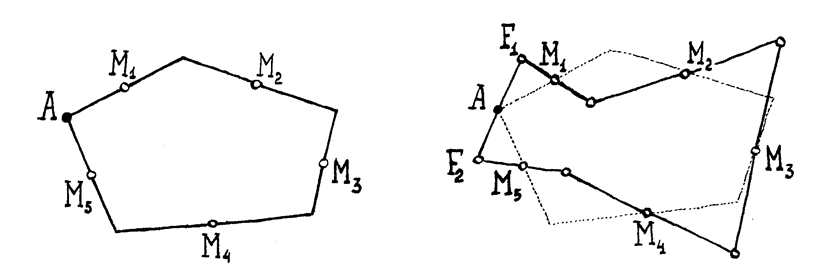
а) Рис.30 б)
Легко убедиться, что при этом отображении точка А
будет неподвижной (перейдет в себя). Согласно выводу в конце §1.5, композиция
нескольких поворотов вокруг разных центров ![]() равносильна
одному повороту на угол 9000 (то есть 1800) вокруг нового
центра. Этим центром будет именно точка А, так как однократный поворот не может
иметь второй неподвижной точки.
равносильна
одному повороту на угол 9000 (то есть 1800) вокруг нового
центра. Этим центром будет именно точка А, так как однократный поворот не может
иметь второй неподвижной точки.
Построение. Взяв произвольную точку F1 (Рис.30, б), построим ее образ F2 в результате пяти последовательных поворотов на углы 1800 вокруг центров М1, М2, М3, М4, М5 . Тогда искомая точка А – середина отрезка [F1F2], так как результирующий поворот на 1800 равносилен симметрии относительно центра А .
Примечание. Решение будет аналогичным в случае любого другого многоугольника с нечетным числом сторон. Для четного числа композиция поворотов характеризуется суммой углов, кратной 3600, а, значит, равносильна тождественному преобразованию. В этом случае неподвижных точек бесконечно много и метод неприменим.
Пример . Построить треугольник, для которого заданные три прямые a, b, c являются серединными перпендикулярами к сторонам.
Анализ. Заданные произвольные три прямые обязательно должны иметь общую точку О – центр окружности, описанной около искомого треугольника АВС (Рис.31, а). Рассмотрим композицию трех симметрий с осями a, b, c.
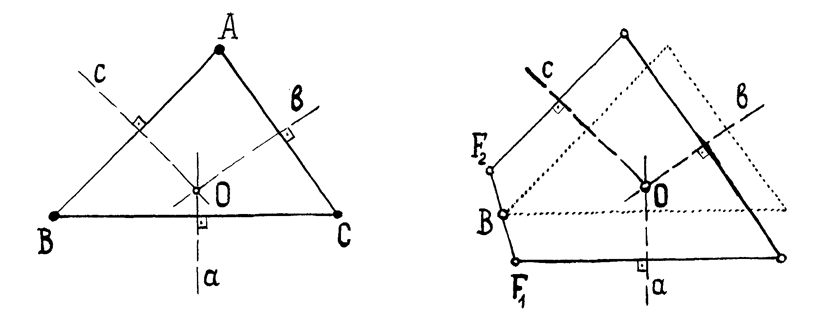
а) Рис. 31 б)
Результирующее движение получится второго рода (то
есть будет скользящим отражением). Но при этом точка О отобразится в себя .
Наличие неподвижной точки для скользящего отражения характеризует его частный
случай – осевую симметрию (см. таблицу 1). Итак, рассматриваемая композиция
равносильна одной осевой симметрии. Ее ось можно построить, если отыскать еще
одну (кроме О) неподвижную точку. Такой точкой будет вершина В (при
последовательных трех симметриях она совершит обход В → С → А → В). Значит,
осью симметрии станет прямая ВО . Итак, ![]() =
=![]() .
.
Построение. Возьмем произвольно точку F1 и найдем ее образ F2
при трехкратной
симметрии ![]() (Рис.31, б). Тогда середина отрезка F1F2
должна дать точку B на результирующей оси ВО. Эта точка В – первая вершина
треугольника, остальные находятся симметрично серединным перпендикулярам а, в,
с. Задача имеет много решений с точностью до подобия.
(Рис.31, б). Тогда середина отрезка F1F2
должна дать точку B на результирующей оси ВО. Эта точка В – первая вершина
треугольника, остальные находятся симметрично серединным перпендикулярам а, в,
с. Задача имеет много решений с точностью до подобия.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.