Итак, симметрия относительно “наклонной” оси gравносильна композиции симметрии Sl c осью Ох и поворота ![]() вокруг
начала координат. Оба эти отображения ранее были описаны в §1.1 . Симметрии
вокруг
начала координат. Оба эти отображения ранее были описаны в §1.1 . Симметрии ![]() соответствуют формулы
соответствуют формулы 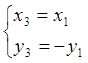 типа
(1), а повороту
типа
(1), а повороту ![]() на угол α=2β вокруг
начала О координат отвечают формулы типа (4):
на угол α=2β вокруг
начала О координат отвечают формулы типа (4): 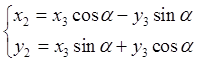 .
Сочетая эти две системы, получим ответ:
.
Сочетая эти две системы, получим ответ:
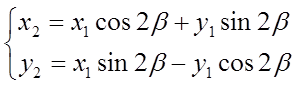 (7)
(7)
(аналитическое представление симметрии с осью, проходящей через начало координат под углом β к горизонту).
Задача 2. Чему равносильна композиция поворота и параллельного переноса?
Решение. Каждую компоненту в композиции ![]() представим
парой осевых симметрий, причем умышленно употребим некоторую ось l
дважды (чтобы сократить в записи выражение Sl
представим
парой осевых симметрий, причем умышленно употребим некоторую ось l
дважды (чтобы сократить в записи выражение Sl![]() Sl = E). Итак, пусть «разложили» поворот
Sl = E). Итак, пусть «разложили» поворот ![]() (где оси lи g
пересекаются в наперед заданной точке О) и параллельный перенос
(где оси lи g
пересекаются в наперед заданной точке О) и параллельный перенос ![]() (где оси lи fобе
перпендикулярны заданному вектору
(где оси lи fобе
перпендикулярны заданному вектору ![]() ) (Рис.18). Тогда
) (Рис.18). Тогда ![]() = (
= (![]() )
)![]() (
(![]() )
=
)
= ![]()
![]()
![]() , то есть получили композицию двух симметрий относительно
непараллельных осей gи
f .
, то есть получили композицию двух симметрий относительно
непараллельных осей gи
f .
|
Рис.18 |
Построение. Проведем ось l через точку О перпендикулярно вектору |
Композиция поворота и параллельного переноса есть поворот на тот же угол около нового центра.
Задача 3. Чему равносильна композиция двух поворотов плоскости вокруг разных центров?
Решение. Каждый из двух заданных поворотов ![]() и
и ![]() представим в виде пары
симметрий, искусственно употребляя некоторую ось l дважды, чтобы подвергнуть
«сокращению»:
представим в виде пары
симметрий, искусственно употребляя некоторую ось l дважды, чтобы подвергнуть
«сокращению»: ![]() = (
= (![]() )
)![]() (
(![]() ) =
) = ![]() .
.
Композиция двух поворотов с несовпадающими центрами равносильна двум осевым симметриям.
Здесь возможны два различных случая, в зависимости от расположения осей fиg.
1)
Они окажутся параллельными
(Рис.19), если сумма углов ![]() =
=![]() (g, l) и
(g, l) и ![]() =
=![]() (f,
l) между парами осей окажется
кратной 1800 (то есть величина
(f,
l) между парами осей окажется
кратной 1800 (то есть величина ![]() кратна
3600). Параллельность осей симметрии соответствует в задаче 1
случаю (б), то есть параллельному переносу. Длина получаемого вектора будет
вдвое больше расстояния между осями fи g, а направление им перпендикулярно.
кратна
3600). Параллельность осей симметрии соответствует в задаче 1
случаю (б), то есть параллельному переносу. Длина получаемого вектора будет
вдвое больше расстояния между осями fи g, а направление им перпендикулярно.
2)
Если же ![]() ≠ kπ (то есть
≠ kπ (то есть ![]() ≠ 2kπ), то получим
пересечение осей fиgв
некоторой новой точке С (Рис.20). Согласно рассуждению из задачи 1 (случай
(в)), точка С станет центром результирующего поворота. При этом угол
≠ 2kπ), то получим
пересечение осей fиgв
некоторой новой точке С (Рис.20). Согласно рассуждению из задачи 1 (случай
(в)), точка С станет центром результирующего поворота. При этом угол ![]() между осями fиgбудет равен
между осями fиgбудет равен
![]() ( внешний угол в треугольнике
( внешний угол в треугольнике ![]() АВС
равен сумме двух внутренних, с ним не смежных). Следовательно, итоговый поворот
произойдет вокруг точки С на угол γ , равный сумме
АВС
равен сумме двух внутренних, с ним не смежных). Следовательно, итоговый поворот
произойдет вокруг точки С на угол γ , равный сумме ![]() углов
двух исходных поворотов.
углов
двух исходных поворотов.
|
|
|
Рис.19 Рис.20
Построение. Проведем прямую lчерез центры А и В заданных
поворотов. Через точки А и В проведем оси fиg(Рис.19, 20) так, чтобы поворот g
→ l происходил
на угол ![]() , а поворот l
→ f - на угол
, а поворот l
→ f - на угол
![]() . Если оси fиg параллельны (Рис.19), то
перпендикулярно к ним строим результирующий вектор
. Если оси fиg параллельны (Рис.19), то
перпендикулярно к ним строим результирующий вектор ![]() (длина
которого вдвое больше расстояния между fи g). Если же оси пересекутся
(Рис.20), то получим центр С нового поворота на угол γ =
(длина
которого вдвое больше расстояния между fи g). Если же оси пересекутся
(Рис.20), то получим центр С нового поворота на угол γ = ![]() .
.
Вывод: 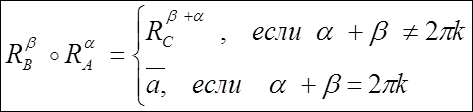
Композиция двух поворотов с
разными центрами есть либо параллельный перенос (если сумма углов кратна 2![]() k), либо
поворот вокруг нового центра на угол, равный сумме углов исходных поворотов.
k), либо
поворот вокруг нового центра на угол, равный сумме углов исходных поворотов.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.