Повторяя многократно рассуждения задачи 3, получим следствие:
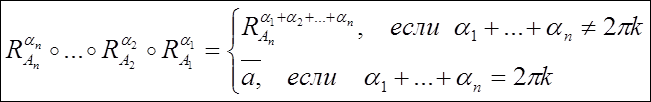
Композиция нескольких поворотов есть либо параллельный
перенос (если сумма всех углов кратна 2![]() k), либо поворот вокруг нового центра на угол, равный сумме
всех углов.
k), либо поворот вокруг нового центра на угол, равный сумме
всех углов.
§ 1.6. Применение движений плоскости к решению задач
Во введении мы приводили фрагмент книги «Начала» Евклида, где доказательство теоремы опиралось на неявное применение движения: мысленно совмещались два треугольника. Подобные рассуждения возникли в глубокой древности. Еще Фалес Милетский (VII в. до Р.Х.), который одним из первых стал употреблять строгие доказательства в геометрии, часто применял методы совмещения фигур. Например, доказывая логически, что диаметр делит круг на две равные части, он фактически мысленно перегибал плоскость по линии диаметра, то есть использовал осевую симметрию. Впоследствии эти соображения были вытеснены из геометрии, которая стала более «статичной». Все, что было связано с «движением», считалось (после парадоксов Зенона) весьма сомнительным и, по возможности, заменялось такими рассуждениями о конгруэнтности, в которых достаточно было сравнивать расстояния между парами соответственных точек фигур. Однако уже в XIX веке идея преобразования плоскости оказалась в теории наиболее важной: неевклидовы геометрии стали рассматривать как наборы свойств фигур, не меняющихся при тех или иных преобразованиях плоскости. Иначе говоря, разные геометрии оказались инвариантами разных групп преобразований.
В элементарной геометрии применение движений часто упрощает решение задач на доказательство, но в еще большей мере – задач на построение. Покажем это на конкретных примерах.
1) Применение осевой симметрии (метод зеркала).
Пример. Даны прямая lи две точки А и В , лежащие от нее по одну сторону. На прямой lнайти точку С такую, чтобы сумма расстояний СА+СВ была наименьшей.
Практический смысл задачи: нужно удачно расположить на шоссе автобусную остановку С (для жителей сел А и В ), чтобы на прокладку дорог СА и СВ потратить как можно меньше материалов.
|
Рис.21 |
Анализ. Если бы точки А и Е лежали по разные стороны от l, то наилучшая ломаная была бы АСЕ, то есть «спрямленная» (Рис.21). Впрочем, для симметричных относительно lточек В и Е расстояния СВ и СЕ равны, поэтому та же точка С дает и min{AC+CB}, значит, является искомой. Доказательство. Любая другая точка С1 будет “хуже”, так как для нее АС1+С1В = АС1+С1Е > АЕ = АС+СЕ = =АС+СВ (знак « > » диктуется неравенством треугольника для АС1Е). Ч.т.д. |
Итак, искомая точка С лежит на прямой АЕ, соединяющей А с зеркальным образом Е точки В.
«Метод зеркала» эффективен не только при отыскании наименьших длин ломаных (путем замены некоторых звеньев на им зеркальные), но и полезен в задачах кинематики, где упругие соударения точек о стену (либо отражения оптических лучей) происходят по принципу «угол падения равен углу отражения». Например, на рис.21 точка С на прямой l, будет единственной, для которой углы наклона отрезков АС и СВ к прямой l равны. Чтобы попасть шайбой А в точку В
после удара о борт l, нужно целиться в зеркальный образ Е точки В .
Типичные задачи на применение зеркальной симметрии:
1) Даны две точки М и К и прямая g , разделяющая их. Через эти точки провести прямые так, чтобы прямая g делила угол между ними пополам. Решение получается мысленным перегибанием плоскости по линии g , так как искомые прямые должны быть относительно нее симметричными. Этими прямыми будут М1К и МК1 , где М1 и К1 – точки «из зазеркалья».
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.