







8.9. Колебания в кулачковых механизмах с упругим толкателем
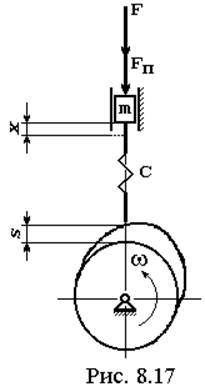 Для исследования
колебаний в кулачковых механизмах с упругим толкателем (выходным звеном)
достаточно рассмотреть одномассовую динамическую модель (рис. 8.17), так как
жесткость кулачкового вала обычно много больше жесткости толкателя.
Рассматривать будем механизм с силовым замыканием. Угловую скорость кулачка w будем считать постоянной. Тогда динамика механизма определяется
дифференциальным уравнением движения массы толкателя, которую можно привести к
одной точке – верхнему концу толкателя. Действие сил упругости толкателя представим
пружиной, помещенной между массой m и кулачком. На массу m
действует внешняя сила F, сила поджимающей пружины FП и сила трения FТ, которую примем пропорциональной скорости верхнего
конца толкателя. Нижний конец толкателя движется в контакте с кулачком, т.е.
перемещение нижнего конца толкателя s, отсчитываемое
от нижнего крайнего положения, определяется профилем кулачка. Перемещение
верхнего конца толкателя x вследствие упругости толкателя отличается от перемещения
s.
Для исследования
колебаний в кулачковых механизмах с упругим толкателем (выходным звеном)
достаточно рассмотреть одномассовую динамическую модель (рис. 8.17), так как
жесткость кулачкового вала обычно много больше жесткости толкателя.
Рассматривать будем механизм с силовым замыканием. Угловую скорость кулачка w будем считать постоянной. Тогда динамика механизма определяется
дифференциальным уравнением движения массы толкателя, которую можно привести к
одной точке – верхнему концу толкателя. Действие сил упругости толкателя представим
пружиной, помещенной между массой m и кулачком. На массу m
действует внешняя сила F, сила поджимающей пружины FП и сила трения FТ, которую примем пропорциональной скорости верхнего
конца толкателя. Нижний конец толкателя движется в контакте с кулачком, т.е.
перемещение нижнего конца толкателя s, отсчитываемое
от нижнего крайнего положения, определяется профилем кулачка. Перемещение
верхнего конца толкателя x вследствие упругости толкателя отличается от перемещения
s.
Сила поджимающей пружины зависит от конструкции. Если место ее крепления расположено ближе к верхнему краю толкателя, то
FП = FО + CПx
где FО – усилие предварительного поджатия,
CП – коэффициент жесткости поджимающей пружины.
Но чаще пружина крепится ближе к нижнему краю толкателя, тогда
FП = FО + CПs
Дифференциальное уравнение движения массы m :
m![]() + h
+ h ![]() + С (x – s) = F + FП + CП
s (
8.24 )
+ С (x – s) = F + FП + CП
s (
8.24 )
где С – коэффициент жесткости толкателя, h – коэффициент демпфирования.
В общем случае уравнение ( 8.24 ) аналитического решения не имеет, так как функция s(j), определяемая профилем кулачка может иметь весьма сложный вид и характер внешней нагрузки F может зависеть от различных параметров и быть тоже функцией любой сложности. Но численное решение этого уравнения дает искомый результат.
8.10. Колебания в механизмах с упругой муфтой
 |
При малых колебаниях в первом приближении характеристику сил упругости в муфте можно считать линейной:
MC = C j, ( 8.25 )
где MC – момент сил упругости, С – коэффициент жесткости, j – угловое смещение полумуфт.
Если упругий элемент 3 имеет нелинейную характеристику, то при достаточно больших углах j применение линейной зависимости ( 8.25 ) может привести к существенным погрешностям в расчетах. Поскольку в таких конструкциях зазоры как правило отсутствуют, а нелинейные жесткостные характеристики упругих элементов представляют собой достаточно гладкие функции, то их можно аппроксимировать полиномами:
C(j) = CO + C1 j + C2 j2 + . . . ( 8.26 )
Тогда момент сил упругости в муфте:
MC = C(j) j. ( 8.27 )
Рассеяние энергии будем считать пропорциональным скорости деформации. При малых колебаниях момент диссипативных сил Мh можно считать:
Mh = h ![]() ,
( 8.28 )
,
( 8.28 )
где h – коэффициент демпфирования,
j – угловая скорость смещения полумуфт.
При больших скоростях для нелинейных упругих элементов в некоторых случаях и демпфирующую характеристику представляют в виде полинома по степеням скорости деформации:
h(![]() ) = hO + h1
) = hO + h1
![]() + h2
+ h2 ![]() 2 + . . . (
8.29 )
2 + . . . (
8.29 )
Тогда момент диссипативных сил в муфте:
Mh = h(![]() )
)![]() .
( 8.30 )
.
( 8.30 )
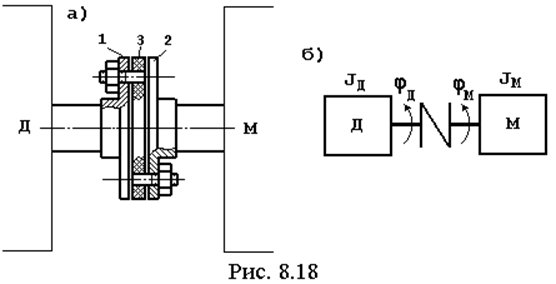
Составим уравнение движения. На рис. 8.18б показана динамическая модель механизма, в котором вал двигателя Д соединен через упругую муфту с валом рабочей машины М. Углы поворота вала двигателя и вала машины обозначены соответственно через jД и jМ. Приведенный к валу рабочей машины момент инерции подвижных частей двигателя JД как правило постоянен. Приведенный момент инерции JМ в общем случае может быть переменным и представлять собой функцию положения JМ = f(jМ).
Так как каждое упругое звено увеличивает общее число степеней свободы на единицу, то число степеней свободы данной системы равно двум.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.