Колебания в кулачковых механизмах с упругим толкателем. Многомассовые колебательные системы при одномерном возбуждении, страница 2

Обозначим через M_Д приведенный к валу двигателя момент движущих сил и через M_С – момент сил сопротивления (с учетом знака). Тогда система уравнений движения при обобщенных координатах  j_Д  и  j_М  имеет вид:

J_ДД  + h + С j   = M_Д

J_ММ  – h – С j + J’_М / 2 = M_С( 8.31 )

где  j  =  j_Д  –  j_М ,  J’_М = dJ_М / dj_М .

Система ( 8.31 ) описывает сразу два разнородных движения: переносное вращение вала приведения и упругие колебания, происходящие как бы относительно этого переносного движения (см. рис. 8.1). Как правило, частоты, характерные для этих процессов сильно отличаются. Переносное вращение происходит с частотами гораздо меньшими, чем упругие колебания. Поэтому решение системы ( 8.31 ) может встретить определенные трудности, связанные с выбором шага (такие системы называют “жесткими”).

В некоторых случаях, например, при достаточно большой мощности двигателя и при постоянном приведенном моменте инерции J_М  удается упростить систему ( 8.31 ). В частности, при достаточно большой мощности двигателя закон движения его ротора j_Д (t)  может считаться не зависящим от изменения  M_С и J_М. Тогда при известной зависимости j_Д (t)второе уравнение системы ( 8.31 ) записывается в виде

                  J_М– h– С j  = M_С –  J_МД,                               ( 8.32 )

т.е. может быть решено относительно углового смещения j независимо от первого уравнения системы ( 8.31 ).

8.11. Многомассовые  колебательные  системы

при  одномерном  возбуждении

Прежде, чем приступить к изучению колебаний в механизмах с упругими валами рассмотрим уравнения дискретных колебательных систем, имеющих прямолинейный характер движения. Мы увидим, что системы уравнений во многом аналогичны.

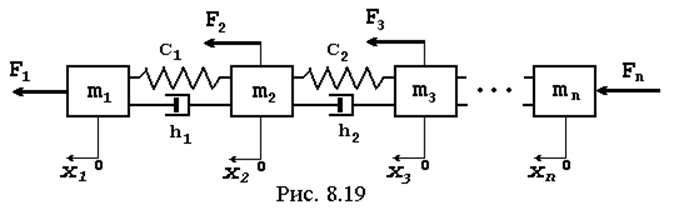На рис. 8.19 представлен довольно распространенный частный случай многомассовой колебательной системы в виде цепной модели. В общем случае массы могут быть соединены упруго-демпфирующими связями в произвольном порядке. Здесь m_i – сосредоточенные массы (i= 1, 2, … n), С_i – коэффициенты жесткости, h_i – коэффициенты демпфирования, F_i – внешние силы, действующие на m_i. Колебания масс будем рассматривать относительно положений их статического равновесия; x_i – смещения масс относительно этих положений.

В общем случае система может быть и нелинейной, тогда жесткостные и демпфирующие параметры будем представлять в виде рядов по степеням соответственно деформации и скорости деформации упругих связей:

C(s) = C_O + C₁ s + C₂ s² +  . . .

h() = h_O + h₁  + h₂ ² +  . . .                                         ( 8.33 )

где s_i  = x_i – x_j – деформация упругой связи между i-й и j-й массами.

Запишем систему дифференциальных уравнений, описывающую колебания системы, изображенной на рис. 8.19. Опираться будем на Принцип д’Аламбера, в соответствии с которым  и  запишем  уравнения  квазиравновесия:

m_{1 1}  + h₁ (₁ – ₂ ) + С₁ (x₁ – x₂ )  = F₁(t),  

  m_{2 2}  + h₂ (₂ – ₃ ) + С₂ (x₂ – x₃ ) + h₁ (₂ – ₁ ) + С₁ (x₂ – x₁ ) = F₂(t),   ( 8.34 )

.  .  .

m_{n n}  + h_n-1 (_n – _n-1 ) + С_n-1 (x_n – x_n-1 )  = F_n(t), 

Преимущества и недостатки таких моделей обсуждались в подразделе 8.1. Решение системы дифференциальных уравнений ( 8.34 ) и является моделированием движения системы под действием внешних сил.

Собственные частоты. Задача определения собственных частот колебательных систем является одной из самых распространенных т.к. во избежание резонансных явлений необходимо сравнивать спектр собственных частот со спектральным составом внешнего воздействия.