Колебания в кулачковых механизмах с упругим толкателем. Многомассовые колебательные системы при одномерном возбуждении, страница 4

Рассмотрим для определенности зубчатый механизм представленный на рис. 8.21а. Для формирования математической модели колебательных процессов используем метод приведения. В качестве звена приведения возьмем вал 1 – вал двигателя.

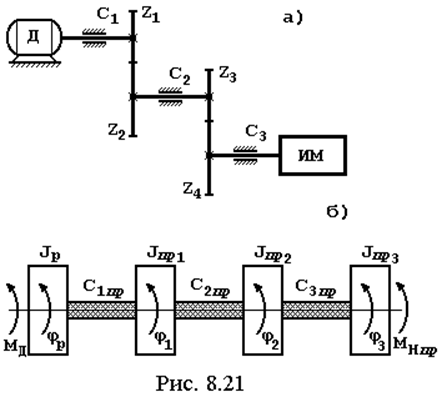
На рис. 8.21б представлена приведенная динамическая модель колебательной системы. Здесь Jp – момент инерции ротора двигателя, J_ИМ – момент инерции исполнительного механизма; J_ПРi– приведенные моменты инерции зубчатых колес и валов:

                                      J_ПР1  = J_Z1+ J_Z2 / i₁₂² ;

                  J_ПР2 =  J_Z3 / i₁₂²  + J_Z4 / (i₁₂² i₃₄²);                                         ( 8.42 )

                                                 J_ПР3 = J_ИМ / (i₁₂² i₃₄²);      

M_Нпр = M_Н / (i₁₂ i₃₄)    – приведенный момент исполнительного механизма.

Система дифференциальных уравнений, описывающая движение такой системы:

J_{Р p}  + h_1ПР  (_p – ₁ ) + С_1ПР (j_p – j₁ )  = M_Д(t),  

 J_{ПР1 1}  + h_2ПР  (₁ – ₂ ) + С_2ПР  (j₁ – j₂ )  + h_1ПР  (₁ – _p ) + С_1ПР  (j₁ – j_p ) = 0,                      

J_{ПР2 2}  + h_3ПР  (₂ – ₃ ) + С_3ПР  (j₂ – j₃ ) + h₂ (₂ – ₁ ) + С_2ПР  (j₂ – j₁ )  = 0,

J_{ПР3 3}  + h_3ПР  (₃ – ₂ ) + С_3ПР  (j₃ – j₂ )  = M_Нпр .                                          ( 8.43 )

Решение системы ( 8.43 ) j₁(t),  j₂(t),  j₃(t),  ₁(t),  ₂(t),  ₃(t) описывает полное движение, которое состоит из “переносного” вращения j_i(t),  w_i(t)  и наложенного на него колебательного движения, вызванного упругостью валов.

Поскольку в данном случае нас интересуют свойства данной системы, как колебательной, то исключим переносное движение, т.е. запишем систему уравнений относительно переносного движения. Для этого перейдем от функций j_i(t)  к функциям

                               y_i(t) = j_i(t) – j_Р(t).                                           ( 8.44 )

Фактически это означает переход к динамической модели, представленной на рис. 8.22, а y_i – это угол поворота i-й массы в колебательном движении. Движение этой модели описывается системой 3-х дифференциальных уравнений, которую получим из 2, 3, 4 уравнений системы ( 8.43 ). Для этого будем последовательно умножать первое уравнение на J_ПРi, i-е уравнение на J_Р (i = 2,3,4) и вычитать из i–го уравнения первое.

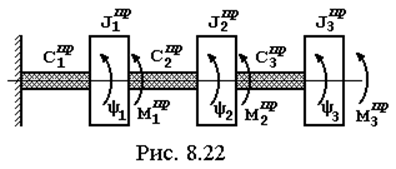Продемонстрируем этот процесс на примере первого и второго уравнений.

 J_РJ_ПР11 + J_Р h_2ПР(_{1  2} ) + J_РС_2ПР (j₁ - j₂ ) + J_Рh_1ПР(₁ - _p ) + J_РС_1ПР(j₁ - j_p ) = 0

¾ 

J_ПР1J_{Р p} + J_ПР1 h_1ПР (_p – ₁ ) + J_ПР1 С_1ПР (j_p – j₁ )  = J_ПР1 M_Д(t),  

¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾ 

J_РJ_ПР1 (₁ – _p) + J_Р h_2ПР (j₁ – j₂ ) + J_Р С_2ПР  (j₁ – j₂ )  +

+ (J_Р + J_ПР1)  h_1ПР (₁ – _p ) + (J_Р + J_ПР1) С_1ПР (j₁ – j_p )  = – J_ПР1 M_Д(t), преобразуем:

обозначим:

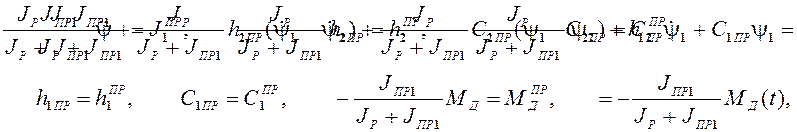Тогда первое уравнение формируемой системы получаем в виде:

J₁^ПР ₁  +  h₂^ПР (₁ – ₂ ) + С₂^ПР(y₁ – y₂ )  +  h₁^ПР ₁  + С₁^ПР y₁   = M₁^ПР  

Остальные уравнения получаем аналогично и вся система запишется как:

J₁^ПР ₁ + h₂^ПР (₁ – ₂ ) + С₂^ПР(y₁ – y₂ ) +  h₁^ПР ₁  + С₁^ПР y₁   = M₁^ПР  

  J₂^ПР ₂ + h₃^ПР (₂ – ₃ ) + С₃^ПР(y₂ – y₃ ) + h₂^ПР (₂ – ₁ ) + С₂^ПР (y₂ – y₁ ) = M₂^ПР                  

J₃^ПР ₃ + h₃^ПР (₃ – ₂ ) + С₃^ПР(y₃ – y₂ )  = M₃^ПР                                             ( 8.45 )

Решение системы ( 2.45 ) y₁(t), y₂(t), y₃(t), ₁(t), ₂(t), ₃(t) описывает чисто колебательное  движение. Нетрудно видеть, что по структуре система (8.45) полностью аналогична системе ( 8.34 ), следовательно программное обеспечение, например пакет NELDER, разработанный для дискретных колебательных систем пригоден для расчета любых дискретных систем как с поступательным, так и с вращательным движением.