Машиностроение \ Теория механизмов и машин

Колебания в кулачковых механизмах с упругим толкателем. Многомассовые колебательные системы при одномерном возбуждении, страница 3

Собственные частоты определяют, рассматривая консервативную модель свободных колебаний. Перепишем систему ( 8.34 ) для n = 3, без учета демпфирующих слагаемых и с нулевой правой частью:

m1 1  + С1 (x1 – x2 ) = 0  

m2 2  + С2 (x2 – x3 ) + С1 (x2 – x1 ) = 0                                               ( 8.35 )

m3 3  + С2 (x3 – x2 ) = 0

Сгруппируем слагаемые при одноименных индексах при x.

m1 1  + С1 x1    –   С1 x2      +    0     = 0  

m2 2  –  С1x1 + (С1 + С2) x2 – С2 x3 = 0                                              ( 8.36 )

m3 3  +   0     –    С2 x2        + С2 x3  = 0

Система ( 8.36 ) записана для конкретной структуры модели. В общем же случае она будет иметь вид:

m1 1  + С11 x1  +  С12 x2  + С13 x3   = 0  

m2 2  +  С21 x1 +  С22 x2  +  С23 x3 = 0                                                ( 8.37 )

m3 3  + С31 x1  + С32 x2  + С33 x3  = 0

Для определения собственных частот составляют так называемое частотное уравнение, которое получается путем раскрытия следующего определителя:

С11 – m1 w12

С12

С13

С21

С22 – m2 w22

С23

= 0

( 8.38 )

С31

С32

С33 – m3 w22

8.12. Колебания  в  зубчатых  механизмах  с  упругими  валами

Вообще говоря, колебательные процессы в зубчатых механизмах обусловлены отнюдь не только упругостью валов. В общем случае это довольно сложная вибро-ударная система, на характер возмущенного движения которой кроме упругости валов оказывают влияние зазоры в зубчатых зацеплениях и муфтах, упругости элементов муфт, упругость зубьев на изгиб и контакт и т.д. В данном подразделе будет рассмотрено моделирование колебательных процессов с учетом только упругости валов.

8.12.1. Приведение  коэффициентов жесткости

упругих  звеньев  механизмов

Приведенным коэффициентом жесткости кинематической цепи называется коэффициент жесткости звена приведения, имеющего ту же потенциальную энергию, что и заменяемая кинематическая цепь. Обратная величина называется приведенным коэффициентом податливости.

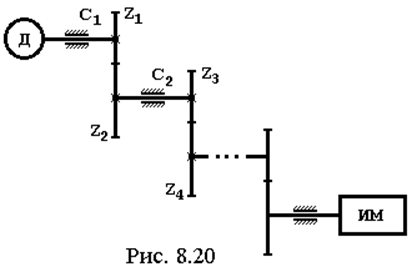
Пусть, например, кинематическая цепь состоит из n последовательно соединенных пар зубчатых колес с упругими валами (рис. 8.20). Обозначим: Сj – коэффициент жесткости звена j, СПР – коэффициент жесткости звена приведения. Если вращающие моменты Мj для звена j, и МПР  для звена приведения выражают только моменты сил упругости:  Мj = Сj Djj ,  МПР = СПР DjПР , (где Djj , DjПР – углы закручивания звена jи звена приведения), то условие равенства потенциальной энергии имеет вид:


                                                    CПР DjПР 2        Cj Djj 2

¾¾¾¾  = S   ¾¾¾

2                            2

или                                                                                                                           ( 8.39 )

МПР DjПР   = S Мj Dj j

Переходя в первом выражении ( 8.39) к дифференциалам получаем:

          CПР   = SCj (djj /djПР )2   =  SCj (wj /wПР )2  =  SCj ij2                         ( 8.40 )

где ij – передаточные отношения.

Аналогично получим выражение для коэффициента податливости:

                               eПР   =  S ej ij2                                                   ( 8.41 )

8.12.2. Уравнения  движения

Скачать файл