Расчёт и проектирование элементов механического пресса с автоматической подачей заготовки. Структурный анализ главного механизма

Изменение реакций в кинематических парах в процессе движения

7. Проектирование вспомогательного механизма

7.1. Компоновка главного и вспомогательного механизма и циклограммирование их совместной работы

7.2. Профилирование кулачка       

7.2.1. Выбор закона движения коромысла

7.2.2. Построение центрового и рабочего профилей

8. Исследование динамики машины.

8.1. Постановка задачи, уравнение движения.

8 2. Результаты математического моделирования и их анализ.

Заключение

Литература

Введение

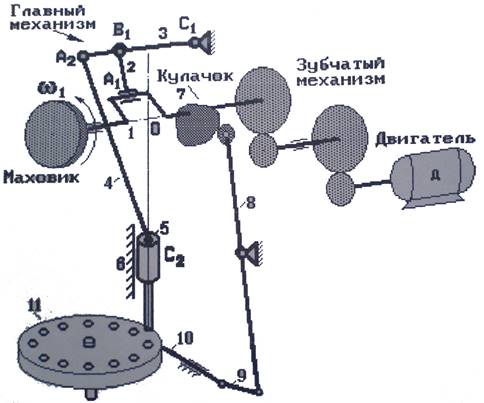
В курсовом проекте исследуется машинный агрегат с автоматической подачей заготовок, структура которого оговорена в техническом задании и схематично представлена на рис. В.1.

1

В проекте решаются следующие задачи:

-  структурный и кинематический анализ главного рычажного механизма

-  выбор двигателя и проектирование зубчатого механизма

-  силовой расчёт главного механизма

-  проектирование механизма подачи заготовок

-  исследование динамических свойств машины и обеспечение требуемой плавности хода.

В состав агрегата входят:

1   – кривошип

2   – шатун

3   – кривошип

4   – шатун

5   – пуансон

7   – кулачок

8   – толкатель

9   – шатун

10 – ползун

11 – револьверный диск

1. Структурный анализ главного механизма

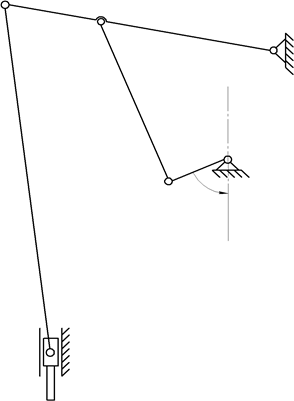
На рис.1.1 представлена структурная схема исполнительного шарнирно-рычажного механизма штамповочного пресса.

В механизме шесть звеньев, из которых пять – подвижные:

1 – кривошип; 2,4 – шатуны; 3 – коромысло; 5 – ползун; 6 – стойка.

	A2
			B1

 

φ1

1

6

C2

C1

A1

O

5

4

3

2

1.1

Эти шесть звеньев образуют семь кинематических пар пятого класса.

В данном механизме отсутствуют пассивные связи.

Число степеней свободы механизма по формуле Чебышева для плоских механизмов:

W = 3n – 2p₅ – p₄ = 3*5 – 2*7 – 0 = 1, где P_k-количество кинематических пар k-го класса, n-число подвижных звеньев.

Определить положение всех звеньев данного механизма можно с помощью одной обобщенной координаты. В качестве обобщенной координаты принят угол поворота кривошипа φ₁.

Входное звено – кривошип:

			O
	1

 

A1

                           W = 3n – 2p₅ – p₄ = 3*1 – 2*1 = 1

                1.2

A2

Структурные группы:

4

6

5

C2

A2

3

B1

2

A1

C1

                           

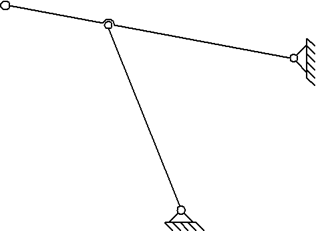
. 1.3

W = 3n – 2p₅ – p₄ = 3*2 – 2*3 = 0

Обе структурные группы имеют 2-й класс и 2-й порядок, следовательно, весь механизм является механизмом 2-го класса, 2-го порядка.

2. Кинематический анализ.

2.1. Постановка задачи

При кинематическом анализе главного механизма будем полагать, что кривошип 1 вращается равномерно с угловой скоростью:

, где n₁ – частота вращения вала кривошипа по техническому заданию.

Началом цикла работы будем считать такое положение механизма, в котором пуансон 5 находится в наивысшей точке. Данному положению соответствует угол поворота кривошипа относительно глобальной системы координат на  Все требуемые расчеты производятся в положении механизма, соответствующем углу поворота относительно глобальной системы координат, в дальнейшем это положение будет называться «расчетным».

Для полного кинематического исследования механизма описанная задача решается для ряда последовательных положений механизма за цикл его работы. На рис. 2.1 представлены планы механизма за цикл его работы, которым является один оборот кривошипа. Началом цикла считается то положение, в котором пуансон 5 находится в крайнем верхнем положении

На . 2.2 представлена схема главного механизма в расчетном положении.

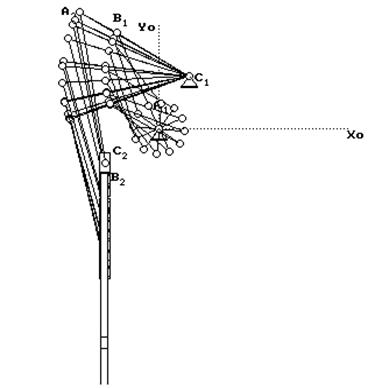
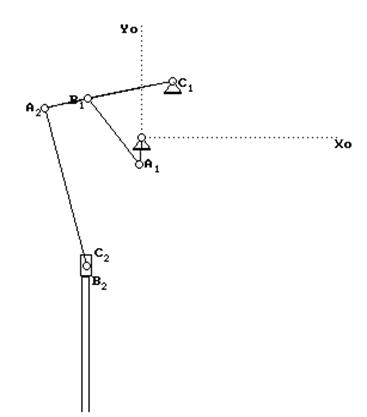
                    . 2.1.                                                   . 2.2.

2.2.1. Метод векторных контуров

Суть метода векторных контуров состоит в следующем. Звенья механизма представляют в виде векторов; поскольку механизм замкнут, то эти векторы образуют замкнутые контуры. Векторные уравнения замкнутых контуров проецируют на оси координат и получают системы алгебраических уравнений для определения кинематических параметров, характеризующих положения звеньев: углов поворота и перемещений. Последовательно дифференцируют эти зависимости, получают уравнения для определения скоростей и ускорений.

Определение кинематических параметров механизма будем производить в соответствии с его структурой, т.е. сначала решим задачу для контура OA₁B₁C₁, а затем для контура С₁A₂B₂.

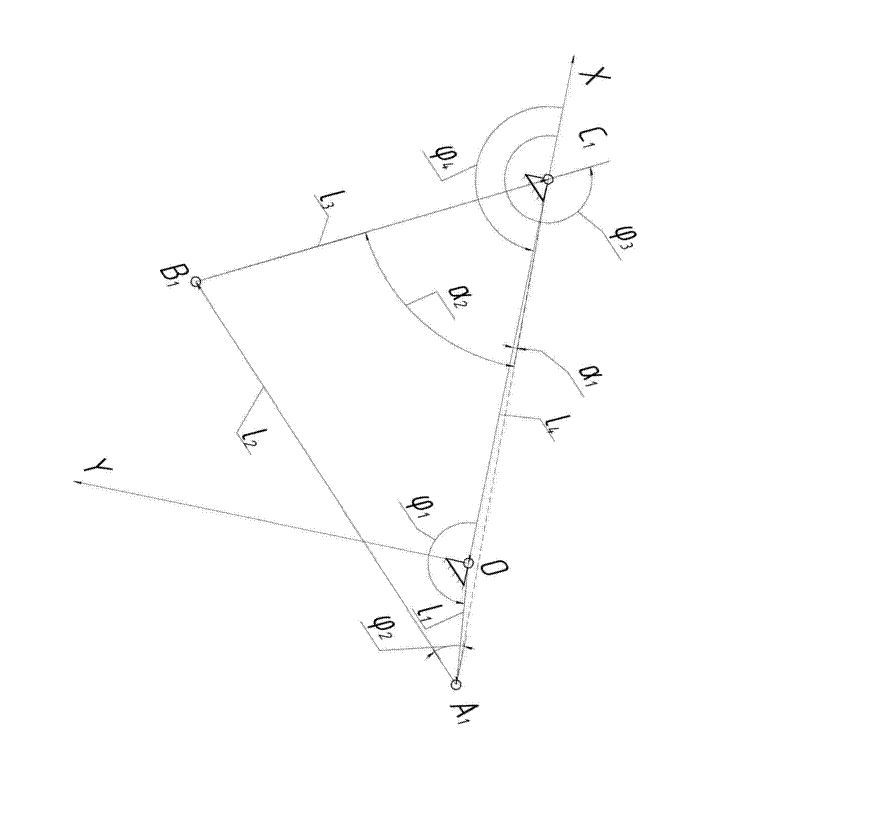            Рассмотрим шарнирный четырехзвенник OA₁B₁C₁. Введем неподвижную систему координат XOY, как это показано на рис. 2.3.

. 2.3.

Уравнение замкнутого векторного контура:

                                                      (2.1)

Проецируя его на оси координат и учитывая, что , получаем [1]:

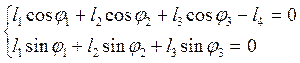,                                          (2.2)

где: l₁ = 0.11, l₂ = 0.34, l₃ = 0.36,

,

, где: - угол поворота шатуна 1, принятый за начало цикла в глобальной системе координат X₀OY₀;  - угол поворота шатуна 1 от начала цикла;  - угол поворота локальной системы координат XOY относительно глобальной системы координат X₀OY₀:

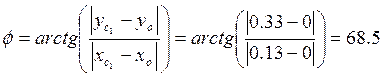
Найдем углы φ₂ и φ₃ [1]:

, где, при условии  [1]:

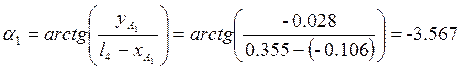, где x_A1, y_A1 - координаты точки А₁:                                 

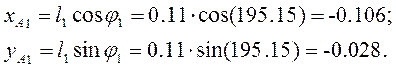
Вычислим угол α₂ [1]:

;

;

;

,

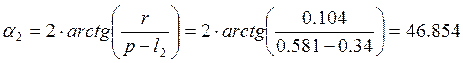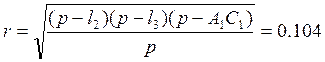При условии, что x_B1>x_A1, найдем угол φ₂ [1]:

;

;

.

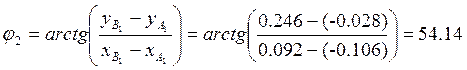Для определения угловых скоростей шатуна A₁B₁ ω₂ и коромысла C₁B₁ ω₃  продифференцируем  систему (2.2) по времени [1]:

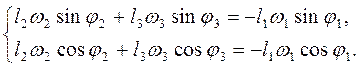                                      (2.3)

Решаем систему (2.3) относительно ω₂, ω₃ и получаем:

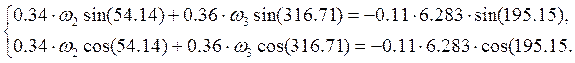
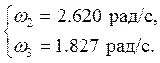
Дифференцируя  систему (2.3) по времени, получаем систему относительно угловых ускорений  и  шатуна