Математическое моделирование транспортного процесса. Метод двойного предпочтения. Распределительная задача, страница 6

Bj Ai                              bj ai		B2 (тыс.т.)		B3(тыс.т.)		B7(тыс.т.)		Bф(тыс.т.)
		90		60		95		265
A1(тыс.т.)	200	22		60	14	95	14	45	100	0	0	8
A2(тыс.т.)	100	90	11	40		40		10		29
								100
A7(тыс.т.)	210	16		47		19		210	100	3	3	3
		5		26		5		0
		6		26		5		0
		6				5

Строим дополнительные строки и дополнительные столбцы.

Находим разницу между двумя наименьшими значениями транспортной ставки в каждой строке и в каждом столбце, полученные результаты записать в дополнительных строках и в дополнительных столбцах. Находим максимальное значение дополнительных строках и в дополнительных столбцах. Это 29. выбираем в строке минимальное значение тарифной ставки и заполняем данную клетку по принципу минимума.

Процесс решения начинается с клетки 2.1 по принципу минимума исходя из условия:

2.1 min {100; 90} = 90 тыс.т.

Процесс повторяем до полного заполнения матрицы.

1.2  min {200;60} = 60 тыс.т.

2.1  min {200 – 60; 95} = 95 тыс.т.

1.4min {200 –  60 – 95; 265} = 45 тыс.т.

2.4 min {100 - 90; 265 - 45} = 10 тыс.т.

3.4 min {210; 265 – 45 - 10} = 210 тыс.т.

После заполнения матрицы приступаем к проверке:

 плана на ограничения:

1 строка 60 + 95 + 45 = 200 тыс.т.

2 строка 90 + 10 = 100 тыс.т.

3 строка 210 = 210 тыс.т.

1 столбец 90 = 90 тыс.т.

2 столбец 60 = 60 тыс.т.

3 столбец 95 = 95 тыс.т.

4 столбец 45 + 10 + 210 = 265 тыс.т.

 на вырождаемость:

план невырождаемый если количество базисных клеток в базе равно сумме строк и столбцов минус единица: Б.К. = m + n– 1 = 3 + 4 – 1 = 6 => план невырождаемый.

 рассчитываем функцию цели:

F = ΣxijCij

После всех расчетов выбрать функцию цели с минимальным значением и решаем эту задачу методом потенциалов.

План оптимальный, если:

• для базисной клетки      ;
• для свободной клетки    ;

В первоначально допустимый план, где функция цели стремится к минимуму вводится дополнительная строка и дополнительный столбец, присваиваем  значение 0. Расчет потенциалов строк и столбцов происходит по базисным клеткам

исходя из условий: .

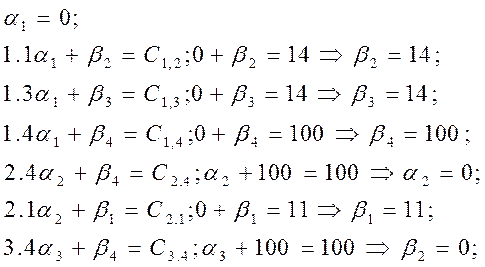
Рассчитав потенциалы строк и столбцов определяем потенциалы свободных клеток.

Если условие   выполняется во всех свободных клетках, то план дальнейшей оптимизации не подлежит.

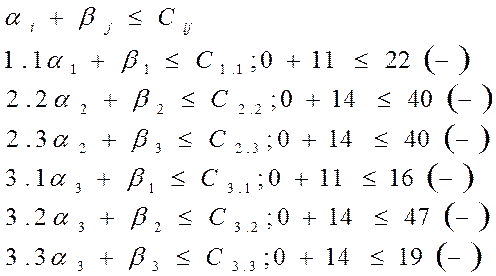
Если условия не выполняются хотя бы в одной клетке, план подлежит оптимизации

путем перераспределения ресурсов внутри матрицы по контуру.                                                

Контур – замкнутая ломаная линия, точки перегибов которой лежат в свободных   

клетках, где максимальная неоптимальность и в базисных клетках. Поворот контура строго по 90º. В контуре расставляем клетки загрузки и разгрузки поочередно начиная со свободной клетки которая подлежит загрузке. Величина загрузки составляет минимальное значение среди клеток разгрузки.

Затем и снова проверка методом потенциалов.