Проверка:
на ограничения:
1 строка 5,3 + 1,5 + 2,2 = 9 единиц
2 строка 9,5 + 0,3 + 3,8+ 0,4 = 14 единиц
3 строка 1,9 + 2,1(резерв) = 4 единиц
1 столбец 9,5 · 21 = 199.5 = 200
2 столбец 0,3 · 23 + 1,9 · 48 = 6,9 + 91,2 = 98,1 = 100
3 столбец 5,3 · 40 = 212 = 210
4 столбец 3,8 · 24 = 91,2 = 90
5 столбец 1,5 · 41 = 61,5 =60
6 столбец 2,2 · 39 + 0,4 · 26 = 85,8 + 10,4 = 96,2 = 95
на вырождаемость:
план невырождаемый если количество базисных клеток в базе равно сумме строк и столбцов минус единица: Б.К. = m + n– 1 = 3 + 6 – 1 = 8 => план невырождаемый.
рассчитываем функцию цели:
F = ΣxijCij
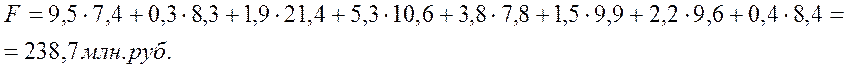
затраты на доставку составили: 238,7 млн.руб.
Третий метод (условной экономии расходов)
1. строим исходную матрицу
2. определить себестоимость в каждой клетке
3. выбираем базисную строчку
4. расчет условной экономии по следующей зависимости
∆Э = Эбj – Sij ∙ πбj
5. находим разницу между двумя наименьшими значениями условной экономии по строкам и по столбцам, разность записать в дополнительные строкам и дополнительные столбцы
6. выбрать максимальное значение условной экономии
7. в строке или в столбце определить клетку с минимальным значением Sij
8. данную клетку загружаем исходя из условий минимума
9. процесс повторять до полного заполнения матрицы
10. проверить план
|
Уч. работ тыс. Тип тонн Флота ед. |
А1 |
А2 |
А7 |
В2 |
В3 |
В7 |
|||||||||||
|
200,0 |
100,0 |
210,0 |
90,0 |
60,0 |
95,0 |
||||||||||||
|
Ф1 |
9 |
0,2 |
0 |
0 |
5,25 |
0 |
2,09 |
0 |
1,46 |
0 |
0 |
0 |
0 |
0 |
|||
|
39 |
40 |
40 |
43 |
41 |
39 |
||||||||||||
|
0,287 |
11,2 |
0,303 |
12,1 |
0,265 |
10,6 |
0,253 |
10,9 |
0,241 |
9,9 |
0,246 |
9,6 |
||||||
|
Ф2 |
14 |
9,63 |
-2,53 |
4,35 |
-2,34 |
-4,12 |
-3,08 |
-3,59 |
0,02 |
-2,3 |
0,53 |
0,53 |
|||||
|
21 |
23 |
25 |
24 |
24 |
26 |
||||||||||||
|
0,352 |
7,4 |
0,361 |
8,3 |
0,368 |
9,2 |
0,325 |
7,8 |
0,329 |
7,9 |
0,323 |
8,4 |
||||||
|
Ф3 |
4 |
-7,36 |
-5,74 |
-9,56 |
-6,86 |
8,76 |
1,93 |
-8,61 |
0,8 |
||||||||
|
51 |
48 |
46 |
53 |
44 |
49 |
||||||||||||
|
0,476 |
24,3 |
0,446 |
21,4 |
0,504 |
23,2 |
0,413 |
21,9 |
0,455 |
20,0 |
0,467 |
22,9 |
||||||
|
2,53 |
2,34 |
4,12 |
3,08 |
3,59 |
2,3 |
||||||||||||
|
2,53 |
2,34 |
3,08 |
3,59 |
2,3 |
|||||||||||||
|
2,53 |
2,34 |
3,08 |
2,3 |
||||||||||||||
|
2,53 |
2,34 |
2,3 |
|||||||||||||||
|
2,34 |
2,3 |
||||||||||||||||
|
2,3 |
|||||||||||||||||
∆Э = Эбj – Sij ∙ πбj
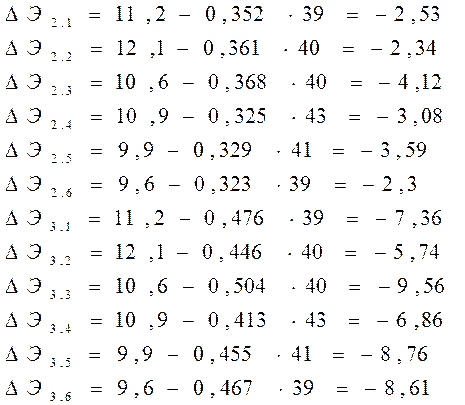
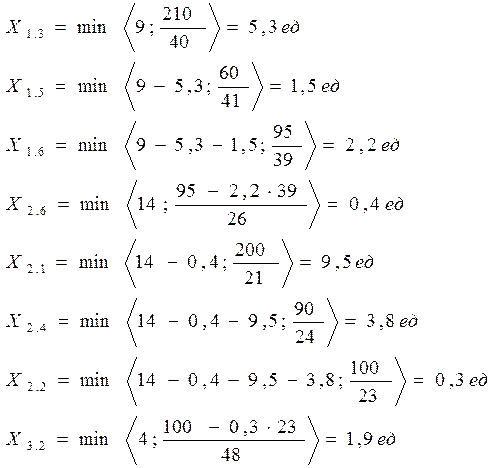
![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.