На рис.2 приведены внешняя статическая характеристика источника питания Uи=f(I)и вольт-амперная характеристика сварочной дуги Uд=f(I). При отсутствии возмущений в системе (dI/dt=O) условие устойчивости (3) соблюдается в точках А и В пересечения xapaктеристик. Проанализируем поведение энергетической системы при малых отклонениях тока. Исследуем на устойчивость процесс горения дуги в точке В. Допустим, что в некоторый начальный момент времени t=0 ток по какой-то причине уменьшился на величину Iо. Этому моменту соответствуют точки В1 и В2 на соответствующих характеристиках. В последующие моменты времени отклонение тока во времени
К определению условия устойчивости системы источник питания - сварочная дуга
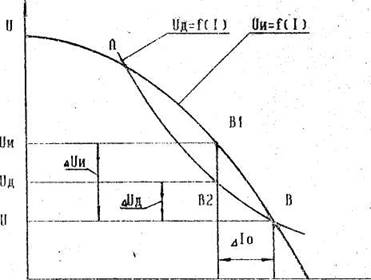
Рис.2
примет текущее значение i. Тогда уравнение (4) для переходного периода будет иметь вид:
Uи(I+i) = Uд(I+i) + L*d(I+i)/dt (5)
Значения Uи(I+i) и Uд(I+i) вблизи точки равновесия В системы определяется выражениями:
Uи(I+i) = U + ∆Uи = U + (dUи/dI)*I = U + Rди*i (6)
Uд(I+i) = U + ∆Uд = U + (dUд/dI)*I = U + Rдд*i (7)
Подставляя (6) и (7) в (5) и преобразовывая, получим:
L*di/dt + (Rдд – Rди)*i = 0 (8)
Разность дифференциальных сопротивлений дуги и источника питания называют коэффициентом (критерием) устойчивости системы Ку. Тогда выражение (8) можно представить в виде:
L'di/dt + Ky*i = 0. (9)
Решая уравнение (9) с учетом начальных условий, т.е. при t=0 i=∆Io, получим закон изменения отклонения тока в зависимости от времени ∆I=f(t)
∆I = ∆Io*exp(-Ky*t/L) (10)
Ранее было отмечено, что система источник питания - сварочная дуга будет находиться в состоянии установившегося равновесия в том случае, если возникшее малое отклонение тока с течением времени будет уменьшаться. В реальных условиях L>0, поэтому для того, чтобы при t→∞ возникшее отклонение тока ∆I→0, необходимо, чтобы Ку был больше нуля. Таким образом, условие устойчивости системы источник питания - сварочная дуга можно сформулировать так: система устойчива, если коэффициент устойчивости системы, равный разности дифференциальных сопротивлений дуги и источника в рабочей точке, положителен:
Ky = Rдд – Rдд = dUд/dI – dUи/dI > 0 (11)
В точке В дифференциальное сопротивление дуги Rдд<0, дифференциальное сопротивление источника также Rди<0, однако по абсолютной величине |Rдд| < |Rди| поэтому Ку>0, т.е. система в точке В устойчива.
Физически это можно объяснить следующим образом. Если, по какой-либо причине ток дуги, соответствующий точке В. уменьшится, то напряжение источника питания окажется больше напряжения на дуге. Это вызовет увеличение напряженности электрического поля в межэлектродном промежутке, ток увеличится до значения I и система вернется в точку В. Наоборот, при случайном увеличении тока напряжение источника питания станет меньше напряжения на дуге, что приведёт к снижению напряжённости поля в дуговом промежутке и, следовательно, к снижению тока. В результате произойдет, восстановление режима горения дуги, соответствующего точке В.
В точке А оба дифференциальных сопротивления также отрицательны, но |Rдд| > |Rди| поэтому Ку<0. Система в точка А неустойчива. Если по какой-то причине произошло увеличение тока, та ток будет возрастать, пока не достигнет значения I, т.е. г. система перейдет к режиму устойчивого равновесия (точка В). Если ток дуги уменьшится, то он будет уменьшаться до тех пор, пока дуговой разряд
Возможные виды статических характеристик источника в зависимости от наклона характеристики дуги
|
|
Рис.3
но прекратится из-за недостаточной величины напряженности электрического поля в дуговом промежутке.
Выполнение условия Ку>0 зависит от соответствия, формы статической характеристики источника вольтамперной характеристике дуги. На рис.3 показаны возможные формы статических характеристик источника питания в зависимости от наклона характеристики дуги.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.