Матричная модель себестоимости. Планирование затрат производства. Основные уравнения (преобразования стоимости)

Матричная модель себестоимости

Планирование затрат производства

, к.т.н.

Предложена и исследована математическая модель преобразования стоимости  в производстве. Модель учитывает цены на сырье, нормы расхода сырья и прогнозные величины косвенных затрат. Известный алгоритм расчета себестоимости предполагает, что выпуск готовой продукции уже свершился и остается распределить прямые и косвенные затраты. Разработанная модель отличается от известной тем, что позволяет произвести расчеты себестоимости не после акта производства, а до него. Таким образом, открывается возможность планирования выпуска производства, оптимального отбора производственных заказов, оптимального выбора рецептур выпуска продукции с учетом сложившихся цен на сырье. Математическая модель работает при любом числе переделов, свободна от коллизий «встречный выпуск полуфабрикатов» и «порядок закрытия подразделений», позволяет автоматически идентифицировать такие ошибки, как  замкнутые циклы движения стоимости.

   Центральным вопросом организации производства является расчет себестоимости. Увидеть ожидаемую прибыль можно только в том случае, если затраты на единицу продукции можно рассчитать наперед до производства продукции и до продажи продукции.

1. Основные уравнения (преобразования стоимости)

  В этом разделе мы даем вывод основных уравнений описывающих преобразование стоимости в производственном процессе. Основным свойством рассматриваемых процессов  является закон сохранения стоимости (материи): стоимость не возникает из ничего, преобразуется и переносится с продукции низших переделов на высшие, не исчезая бесследно. Например, закон работает в материальном производстве и известен как метод двойной записи Луки Пачоли, положивший начало современной бухгалтерии. 

Прогнозный расчет себестоимости становится возможным, если известны нормы расхода входящих ресурсов на единицу получаемой продукции. Связь «входящие ресурсы-нормы – продукция», по определению норм расхода, представляется векторным уравнением:

X = AZ ,  (1) где

• X- n-мерный вектор количества входных ресурсов;
• A - матрица размера n x m норм расхода входных ресурсов на производство единицы продукции;
• Z - m-мерный вектор количества выходных ресурсов.

Согласно закону о сохранении стоимости, в процессе производства стоимость входных ресурсов совпадает со стоимостью выходных ресурсов. Стоимость израсходованных ресурсов представляется стандартным скалярным произведением (X,S) вектора количества входных ресурсов X и вектора цен входящих ресурсовS в n-мерном евклидовом пространстве. Стоимость продукции также есть скалярное произведение (Z,R) вектора количества выходных ресурсов Z и вектора себестоимости R. Приравнивая скалярные произведения, получаем уравнение баланса стоимости:

  (X,S) = (Z,R)  (2)

Мы получили аналог уравнения двойной записи Луки Пачоли, который означает, что стоимость входных ресурсов полностью перенеслась на продукцию. Это уравнение и является математическим выражением закона сохранения стоимости (материи).

Таким образом, система уравнений (1) и (2) формализует задачи планирования затрат производства. Формула (1) определяет потребность в ресурсах X при заданных плане выпуска Z и матрице норм A. Уравнение (2), решенное относительно R, позволяет определить себестоимость единицы продукции.

  Поставленная задача не имеет единственного решения. Приведем следующие решения:

 R_i = (X,S)/Z_i (2a)

  R=(X,S)/(Z,1)  (2b) 

  R=(X,S)*Z/(Z,Z)   (2с)

Для построения решения преобразуем левую часть уравнения (2), подставив в нее уравнение (1):

(X,S) = (AZ,S)

Используя тождество

(AZ , S)=(Z , A^T S)

где A^T- транспонированная матрица, преобразуем уравнение (2) к виду:

  (Z , A^T S) = (Z,R)

Откуда следует решение:

  R= A^T S  (3)

В случае одномерного вектора продукции (m=1) это решение полностью совпадает с известным решением. Действительно, как следует из уравнения баланса (2)

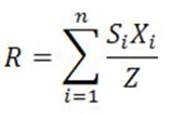
Так как 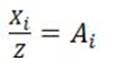- есть норма расхода i-го вида ресурсов на производство единицы продукции, то решение преобразуется к виду (3). Наш выбор решения (3) основан на том, что оно полностью совпадает с решением для одномерной модели (m=1).

Решения (2b) и  (2c) неприменимы для случаев, когда модель производства многомерна (m>1) и при этом продукция измеряется в разных единицах (например, и в километрах, и в килограммах, и в штуках), так как сложение величин различной физической размерности не имеет смысла.