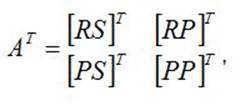
Экономика и менеджмент \ Бухгалтерский учет

Матричная модель себестоимости. Планирование затрат производства. Основные уравнения (преобразования стоимости), страница 3

откуда следует

 (3a)

  

 (3b)

 

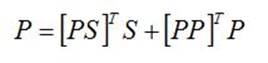
Таким образом, при заданных векторе  и матрице норм, состоящей из четырех блоков , , ,  из уравнений (3a) и (3b) следует определить неизвестные вектора R и P.

Уравнения (1a),(1b) и (3a),(3b) являются линейными и сопряженными.

Для решения уравнений (1b) и (3b) можно применить как метод формального решения системы линейных алгебраических уравнений (например, метод Гаусса [Гантмахер, стр.39], так и метод простых итераций.

Метод простых итераций очень интересен тем, что каждой итерации отвечает передел. При производстве первого полуфабриката на первом переделе используется только сырье. Это означает, что подставив в правую часть уравнений P = 0 , мы получим стоимость полуфабрикатов и продукции первого передела.

 На втором переделе производство потребляет  полуфабрикаты первого передела. Подставляя в правую часть уравнений (3a)-(3b) результаты первой итерации, получим стоимость полуфабрикатов второго передела. Метод простых итераций естественным образом моделирует многопередельный производственный процесс. Каждая итерация представляет переход от передела к переделу. При этом задача о потребности сырья в ресурсах решается в обратном порядке - начиная с последнего передела, который для уравнений (1a)-(1b) имеет смысл плана выпуска продукции, и заканчивая первым переделом, в котором сырье преобразуется в полуфабрикат первого передела.

Итерационное решение уравнений (1a) и (1b) можно представить как формальное разложение обратной матрицы в ряд геометрической прогрессии по степеням матрицы РР.

Так как

 (E – PP)-1 = E + PP +…+PPN-1+… , то (1b) принимает вид

Y= (E – PP)-1[RP]Z

Или

Y = (E + PP+…+PPN-1+…)[RP]Z

Первый член этого ряда представляет последний передел и равен вектору количества полуфабрикатов, используемых в завершающей фазе производства. Второй член ряда равен количеству полуфабрикатов предпоследнего передела, и так далее.

Подставляя найденное значение Y в  (1a), получаем:

   X =[RS]Z + [PS]*(E + PP+…PPN-2+…)

  Указанные ряды являются сходящимися при условии, что спектральный радиус оператора РР меньше единицы. Таким образом, разрешимость уравнений, описывающих нашу матричную модель, зависит от значений собственных чисел матричного блока PP, отвечающего за преобразование полуфабрикатов в полуфабрикаты. Выделим следующие случаи:

1) спектральный радиус (максимальное собственное значение) l больше единицы;

2) спектральный радиус  l равен единице;

3) спектральный радиус  меньше единицы;

4) спектральный радиус равен нулю.

  Разберем выделенные случаи.

1)  В первом случае итерационным способом решение не может быть построено. Известный ряд Неймана является бесконечным и расходится как геометрическая прогрессия с основанием более единицы.  В то же время формальное решение существует (может быть получено методом Гаусса) и является единственным, так как матрица системы уравнений не вырождена.  Однако решение и уравнения ресурсов (1b), и уравнения стоимости (3b) имеют отрицательные компоненты. Это следует из спектрального представления решения, получаемого путем разложения по собственным векторам. Таким образом, если матричный блок  PP имеет собственные числа более единицы, то следует говорить об ошибке в формировании матрицы норм. Такое материальное производство существовать не может. По таким законам может развиваться образовательный процесс, когда число обучаемых растет в геометрической прогрессии (евангельская легенда о насыщении 5000 человек пятью ячменными хлебами и двумя рыбками, когда после трапезы еды осталось 12 коробов - больше, чем было вначале) или  финансовая пирамида, но не материальное производство. Проиллюстрируем появление решений с отрицательной компонентой на примере двумерной матрицы  PP.

Рассмотрим матрицу

 

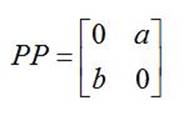
c собственными числами  . Нулевые значения на главной диагонали означают, что для выпуска полуфабриката сам полуфабрикат  не может быть входным ресурсом. Тогда матрица системы уравнений  (1b)   равна 

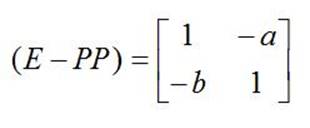
Обратная матрица имеет вид

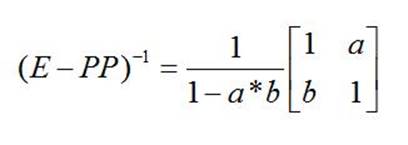
Очевидно, что при условии  ab>1,a>0,b>0  все компоненты решений уравнений (1b) и уравнения (3b) отрицательны. Отрицательные значения принимают как компоненты вектора  потребности в сырье, так и вектора себестоимости.  Следовательно, формальное решение системы линейных уравнений не может отражать материального производства, так как отрицательные значения не имеют экономического смысла.

Скачать файл